5. Fractions Partielles et fonctions rationnelles
Les fonctions rationnelles que nous allons intégrer doivent avoir le coefficient du numérateur plus petit que celui du dénominator.
En plus de cette condition, si on met le dénominateur en facteurs, nous obtenons les fractions partielles.
![]()
Il se peut que lorsqu’on considère que ![]() ,
,
Le rapport devient:
![]()
C’est un facteur linéaire de Fractions partielles.
On doit avoir en memoire les deux formules qui suivent:
![]()
![]() with
with ![]()
Problème 28
Evaluer:
![]()
On met le dénominateur en facteurs:
![]()
![]()
![]()
Pour ![]()
![]()
Pour ![]()
![]()
De retour sur le rapport:
![]()
Sur l’évaluation:
(1) 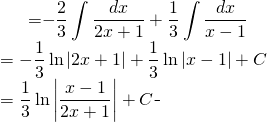
Finalement:
![Rendered by QuickLaTeX.com {\displaystyle \int \frac{dx}{2x^{2}-x-1} }={\displaystyle \frac{1}{3} \ln \left | \frac{x-1}{2x+1} \right |+C}={\displaystyle \ln \left |\sqrt[3]{ \frac{x-1}{2x+1}} \right |+C}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-39b9af881c5da4572b302acc6ae9e8a9_l3.png)
Problème 29
Evaluer:
![]()
On met le dénominateur en facteurs:
![]()
![]()
![]()
Si ![]()
![]()
Si ![]()
![]()
![]()
Du retour au rapport:
![]()
Du retour sur l’évaluation:
(2) 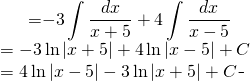
Finalement:
![]()
Problème 30
Evaluer:
![]()
On met le dénominateur en facteurs:
![]()
![]()
Si ![]()
![]()
![]()
Quand on remplace:
![]()
Le terme en ![]()
![]()
Du retour sur le rapport:
![]()
Sur l’évaluation:
(3) 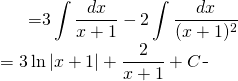
Finalement:
![]()
Problème 31
Evaluer:
![]()
On met le dénominateur en facteurs:
![]()
Le dénominateur commun aux deux membres ![]() :
:
Nous obtenons ce qui suit:
![]()
Soit ![]()
Seulement le facteur de ![]() compte:
compte:
![]()
Ce qui donne:
![]()
Soit maintenant ![]()
Seul le facteur de ![]() compte:
compte:
![]()
Ce qui donne:
![]()
On remplace ![]() et
et ![]() ci-dessous:
ci-dessous:
![]()
![]()
![]()
![]()
![]()
Pas de terme en ![]() :
:
Nous avonst:
![]()
On tire: ![]()
We can now take the terms in ![]() :
:
![]()
Mais ![]()
![]()
![]()
![]()
![]()
Alors ![]()
Ce qui prouve aussi que: ![]() est vrai.
est vrai.
De retour sur le rapport:
![]()
![]()
Sur l’évaluation:
(4) 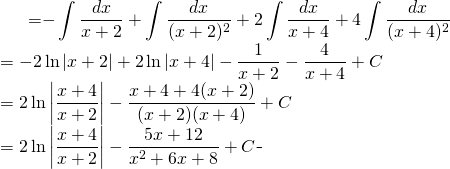
Finalement:
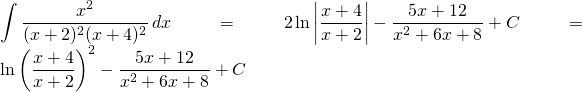
Problème 32
Evaluer:
![]()
On met le dénominateur en facteurs:
![]()
On aura:
![]()
LCM des deux membres au dénominateur ![]() :
:
On aura:
![]()
Soit ![]()
Seul le facteur de ![]() compte:
compte:
![]()
Ce qui donne:
![]()
De retour sur l’équation:
![]()
![]()
Pour les termes en ![]()
![]()
![]()
pour les constants:
![]()
![]()
On peut vérifier avec le coefficient en ![]() .
.
De retour sur le rapport:
![]()
Sur l’évaluation:
![]()
Nous savons que:
![]()
De ![]()
![]()
Nous avons aussi que:
![]()
(5) 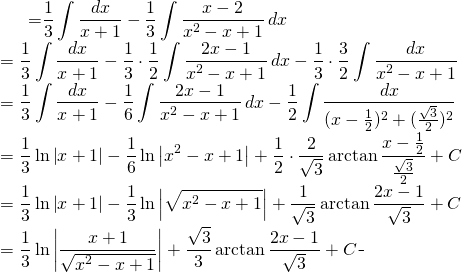
Finalement:
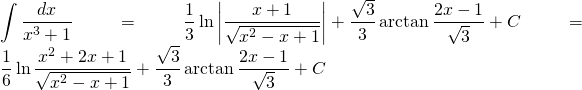
Problème 33
Evaluer: ![]()
Problème 19 repris avec les fractions partielles.
Nous savons que:
![]()
On met le dénominateur en facteurs:
![]()
LCM des 2 membres au dénominateur ![]() :
:
On obtient ce qui suit:
![]()
Soit ![]()
Seul le facteur en ![]() compte:
compte:
![]()
Soit ![]()
Seul le facteur en ![]() compte:
compte:
![]()
De retour sur l’équation:
![]()
On décompose:
![]()
![]()
![]()
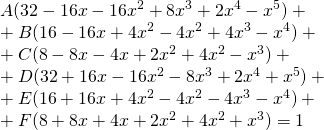
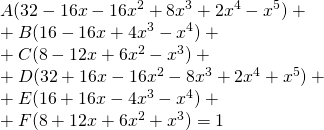
Pour les termes en ![]()
![]()
Pour les termes en ![]()
![]()
Pour les termes ![]()
![]()
Mais ![]() et
et ![]()
![]()
![]()
Pour les termes en ![]()
![]()
Comme ![]()
![]()
Mais ![]()
![]()
![]()
Mais nous avons vu que ![]()
Ce qui donne:
![]()
![]()
En resumé:
![]()
![]()
![]()
![]()
![]()
![]()
De retour sur le rapport:
![]()
Sur l’évaluation:
(6) 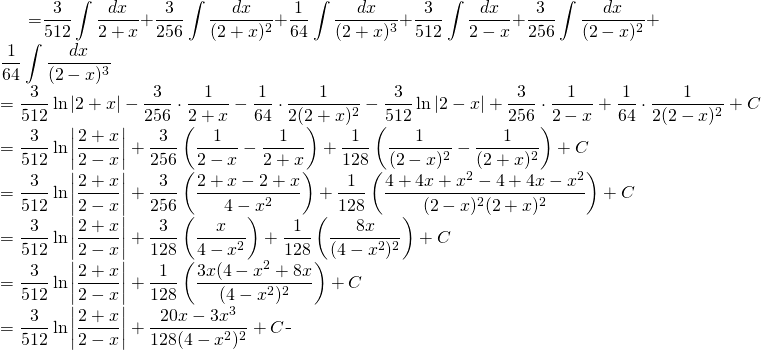
Finalement:
![]()


Be the first to comment