6. Intégration des fonctions irrationnelles
Les fonctions irrationnelles sont un peu difficile à intégrer. Il y a des cas qui nécessitent des techniques spécifiques.
Les techniques varient avec la situation. Heureusement que nous les avons citées plus haut.
Cas 1: Exposants en fractions
Beaucoup de fonctions irrationnelles seront combinées.
Problème 34
Evaluer: ![]()
On pourra avoir les exposants de la forme:
![]()
Nous cherchons le dénominateur commun de toutes les fractions en exposants.
Ici nous avons seulement deux ![]() and
and ![]()
le dénominateur commun ici est de 4.
Soit ![]()
![]()
![]()
![]()
Nous aurons
![]()
En divisant:
![]()
![]()
![]()
![]()
De retour sur ![]() :
:
![]()
Finalement:
![]()
Problème 35
Evaluer: ![]()
On écrit les exposants comme suit:
![]()
Les fractions sont: ![]() ,
, ![]() and
and ![]()
Le dénominateur commun est PPCM de 6 et 4. C’est 12.
Soit ![]()
![]()
![]()
![]()
Soit maintenant:
![]()
![]()
Pour ![]()
![]()
Les termes ![]()
![]()
![]()
![]()
Les termes en ![]() :
:
![]()
![]()
![]()
![]()
Les termes en ![]()
![]()
![]()
![]()
On a:
![]()
(1) 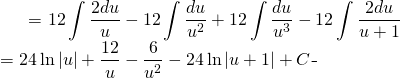
De retour sur ![]()
Nous savons que ![]()
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{\sqrt[6]{x}+1}{\sqrt[6]{x^{7}}+\sqrt[4]{x^{5}}} \, dx}&= {\displaystyle 24 \ln \left | x^{\frac{1}{12}} \right |+\frac{12}{x^{\frac{1}{12}}}-\frac{6}{(x^{\frac{1}{12}})^{2}}-24 \ln \left |x^{\frac{1}{12}}+1 \right | +C}\\ &= {\displaystyle 24 \ln \left |\sqrt[12]{x} \right |+\frac{12}{\sqrt[12]{x}}-\frac{6}{\sqrt[6]{x}}-24 \ln \left |\sqrt[12]{x}+1 \right | +C} \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-2fa983dcb4e322502e28307efed1c7ad_l3.png)
Finalement:
![]()
OU
![]()
Cas 2: Une seule fraction avec un exposant sous forme de fraction
![]()
Nous utiliserons la relation suivante:
![]()
Problème 36
Evaluer: ![]()
Soit ![]()
![]()
![]()
![]()
![]()
![]()
Nous aurons:
(3) 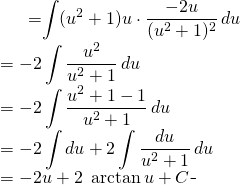
De retour sur ![]()
![]()
Finalement:
![]()
Problème 37
Evaluer: ![]()
Soit ![]()
![]()
![]()
Nous avons:
(4) 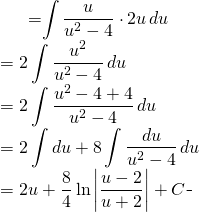
De retour sur ![]()
![]()
Finalement:
![]()
Cas 3: Foction irrationnelle au dénominateur avec un polynôme au numérateur
Nous l’avons vu plus haut :
La forme est de:
![]()
Problème 38
Evaluer: ![]()
Nous savons que:
![]()
Aussi:
![]()
![]()
De ![]()
![]()
De retour sur l’évaluation:
(5) 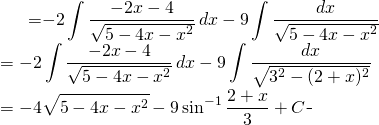
Finalement:
![]()
Cas 4:D’autres formes irrationnelles
Problèmes du type ![]() ,
,![]() or
or ![]()
Nous avons vu que:
Pour ![]() , nous avons une substitution trigonométric avec
, nous avons une substitution trigonométric avec ![]() OU
OU ![]()
Pour ![]() , nous avons une substitution trigonométric avec
, nous avons une substitution trigonométric avec ![]() OU
OU ![]()
Pour ![]() , nous avons une substitution trigonométric avec
, nous avons une substitution trigonométric avec ![]() OU
OU ![]()
Pour la forme:
![]()
Utiliser:
![]()
Si la quadratique a des racines et peut se factoriser:
![]() , we can use
, we can use ![]()
Si ![]()
![]() , we can use
, we can use ![]()


Be the first to comment