Techniques d’Integration , pages multiples

7. Intégrales trigonométriques et hyperboliques

Les formules trigonométriques connues seront utilisées.

On se concentre sur les techniques.

Cas contenant 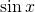$\sin x$ and $\cos x$

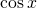
On procède comme suit:

$\tan \frac{x}{2}=t$

On peut montrer que:

$\sin x=\frac{2t}{1+t^{2}}$

$\cos x=\frac{1-t^{2}}{1+t^{2}}$

$x=2 \arctan t$

$dx=\frac{2dt}{1+t^{2}}$

Ce qui nous ramène aux intégrales normales.

Cas de la forme $\int \sin^{m} x \cos^{n} x\, dx$

-Si $m$ est impair, utilser $u=\cos x$ .

-Si $n$ est impair, utiliser $u=\sin x$ .

Cas de la forme $\int \tan^{m} x \sec^{n} x\, dx$

-Si $m$ est IMPAIR, utiliser $u=\sec x$ .

-Si $n$ est PAIR, utilser $u=\tan x$ .

Problème 39

Evaluer: $\int \sin^{3} x \, dx$

Nous voyons que:

$\sin^{3} x=\sin^{2} x \sin x =(1-\cos^{2} x) \sin x$

Soit $u=\cos x \Rightarrow du=-\sin x \, dx$

${\displaystyle \int \sin^{3} x \, dx}= {\displaystyle -\int (1-u^{2})\,du }\\={\displaystyle -\int du+\int u^{2}\,du }\\=-u+\frac{u^{3}}{3}+C=-\cos x+\frac{1}{3} \cos^{3}x+C$

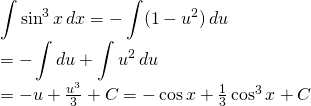
Finalement:

$\int \sin^{3} x \, dx}={\displaystyle -\cos x+\frac{1}{3} \cos^{3}x+C$

Problème 40

Evaluer: $\int x \arcsin x \, dx$

Intégration par parties:

Soit $u=\arcsin x \Rightarrow du=\frac{dx}{\sqrt{1-x^{2}}}$

$dv=xdx \Rightarrow v=\frac{1}{2}x^{2}$

Nous avons

$\int x \arcsin x \, dx }={\displaystyle \frac{1}{2}x^{2} \arcsin x-\frac{1}{2}\int \frac{x^{2} \,dx}{\sqrt{1-x^{2}}}$

Soit:

$I= -\frac{1}{2}\int \frac{x^{2} \,dx}{\sqrt{1-x^{2}}}$

Substitution trigonométrique :

Soit $\sin \theta=x \Rightarrow dx=\cos \theta \, d\theta$

$\cos \theta=\sqrt{1-x^{2}}$

$\theta=\arcsin x$

(1) $\begin{equation*} \begin{split} I&= {\displaystyle -\frac{1}{2}\int \frac{x^{2} \,dx}{\sqrt{1-x^{2}}} }\\ &={\displaystyle -\frac{1}{2}\int \frac{\sin^{2} \theta \cos \theta \, d\theta}{\cos \theta} }\\ &= {\displaystyle -\frac{1}{2}\int \sin^{2} \theta \, d\theta }\\ &={\displaystyle -\frac{1}{4}\int (1-\cos 2\theta) \, d\theta }\\ &={\displaystyle -\frac{1}{4} \theta+\frac{1}{8}\sin 2\theta +C}\\ &={\displaystyle -\frac{1}{4} \theta +\frac{1}{4}\sin \theta \cos \theta +C}\\ &= {\displaystyle -\frac{1}{4} \arcsin x +\frac{1}{4}x \sqrt{1-x^{2}}+C} \end{split} \end{equation*}$

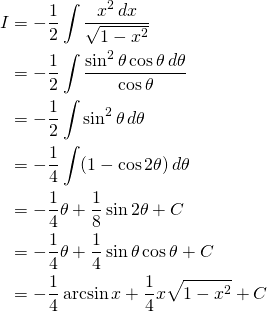
De retour sur l’original:

$\int x \arcsin x \, dx }={\displaystyle \frac{1}{2}x^{2} \arcsin x-\frac{1}{4} \arcsin x +\frac{1}{4}x \sqrt{1-x^{2}}+C$

$\int x \arcsin x \, dx }={\displaystyle \frac{1}{4}(2x^{2}-1) \arcsin x+\frac{1}{4}x \sqrt{1-x^{2}}+C$

Finalement:

$\int x \arcsin x \, dx }={\displaystyle \frac{1}{4}(2x^{2}-1) \arcsin x+\frac{1}{4}x \sqrt{1-x^{2}}+C$

Problème 41

Evaluer: $\int \cos^{6} x \, dx$

$\int \cos^{6} x \, dx }={\displaystyle \int (\cos^{2} x)^{3} \, dx$

$\int (\cos^{2} x)^{3} \, dx }={\displaystyle \int (\frac{1+\cos 2x }{2})^{3} \, dx$

$\int (\frac{1+\cos 2x }{2})^{3} \, dx }={\displaystyle \frac{1}{8} \int (1+\cos 2x)^{3} \, dx$

En rendant plus facile:

(2) $\begin{equation*} \begin{split} \displaystyle (1+\cos 2x)^{3} }&= {\displaystyle 1+ 3\cos 2x + 3 \cos^{2} 2x+ \cos^{3} 2x}\\ &={\displaystyle 1+ 3\cos 2x+ 3 \frac{1+\cos 4x}{2}+ (1-\sin^{2} 2x)\cos 2x }\\ &={\displaystyle 1+ 3\cos 2x+ \frac{3}{2}+ \frac{3}{2}\cos 4x+\cos 2x- \sin^{2} 2x \cos 2x }\\ &={\displaystyle \frac{5}{2}+ 3\cos 2x+ \frac{3}{2}\cos 4x+\cos 2x- \sin^{2} 2x \cos 2x } \end{split} \end{equation*}$

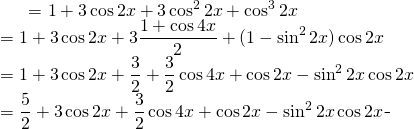
De retour sur l’Equation:

(3) $\begin{equation*} \begin{split} \displaystyle \int \cos^{6} x \, dx }&={\displaystyle \frac{1}{8} \int (1+\cos 2x)^{3} \, dx }\\ &={\displaystyle \frac{1}{8} \cdot \frac{5}{2} \int dx+\frac{1}{8} \cdot 4 \int \cos 2x \,dx+ \frac{1}{8} \cdot \frac{3}{2} \int \cos 4x \,dx- \frac{1}{16} \int 2\sin^{2} 2x \cos 2x \,dx }\\ &={\displaystyle \frac{5}{16} x+ \frac{4}{16} \sin 2x+ \frac{3}{64} \sin 4x-\frac{1}{48}\sin^{3} 2x+ C}\\ &={\displaystyle \frac{1}{16} \left [ 5x+ 4\sin 2x+ \frac{3}{4} \sin 4x-\frac{1}{3}\sin^{3} 2x \right ]+ C} \end{split} \end{equation*}$