2.Integration by parts
This is the technique of transforming one integral into another that is easier to evaluate.
The integration by parts comes from the following derivatives formula:
![]()
This can be written:
![]()
Taking the indefinite integral of both side we get:
![]()
Or simply:
We must make an adequate choice in order not to get a more complicated integrated.
One of the favorite examples is:
Evaluate ![]()
Let ![]()
![]()
![]()
Problem 13
Evaluate: ![]()
Let ![]()
![]()
We get:
(1) 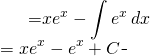
Finally:
![]()
Problem 14
Evaluate: ![]()
Let ![]()
![]()
We write:
(2) 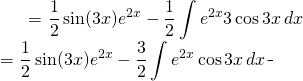
We resume the process for the second part of the integral:
Let ![]()
![]()
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int e^{2x} \sin 3x\, dx}&={\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{2}[\frac{1}{2} \cos (3x) e^{2x}+\frac{3}{2}\int e^{2x} \sin 3x\, dx]}\\ &= {\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{4}\cos (3x) e^{2x}-\frac{9}{4}\int e^{2x} \sin 3x\, dx \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-13a3be41feca8ab983f8c3a34c8774a5_l3.png)
We are back to a fraction of the original:
![]()
![]()
![]()
![]()
Finally:
![]()
Problem 15
Evaluate: ![]()
Let ![]()
![]()
We write:
(4) 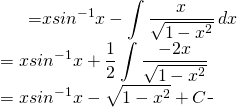
Finally:
![]()
Problem 16
Evaluate: ![]()
Let ![]()
![]()
We write:
![]()
We resume:
Let ![]()
![]()
Back to the original equation:
![]()
![]()
![]()
![]()
Finally:
![]()
Problem 17- Special Case
Evaluate: ![]()
When ![]() is a large natural number,we decrease
is a large natural number,we decrease ![]() by
by ![]() to case a situation where we have to integrate
to case a situation where we have to integrate ![]()
We proceed as follows:
Let ![]()
![]()
We get:
![]()
Or:
![]()
![]()
We find the original integral in the right part. We group and we get:
![]()
![]()
We get:
![]()
This is very useful when combined with our know formula:
![]()
Problem 18
Evaluate: ![]()
Let ![]()
Or:
![]()
![]()
We get:
![]()
Now, just for fun
![]()
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Back to the original equation:
![]()
![]()
Finally:
![]()


Be the first to comment