3. Trigonometric substitution
The following algebraic expressions when involved in the integrands, we need to use the method of trigonometric substitution:
![]()
![]()
![]()
Trigonometric cases
| Integral Involving | Use Substitution | Then Identity |
Or Hyperbolic substitution:
| Integral Involving | Use Substitution | Then Identity |
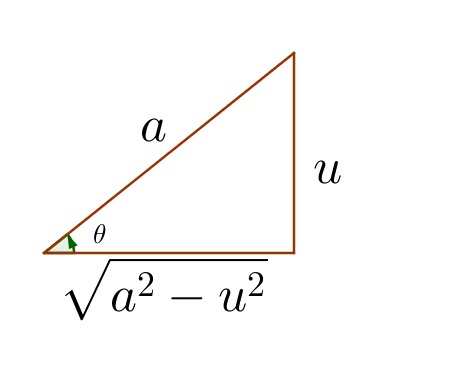
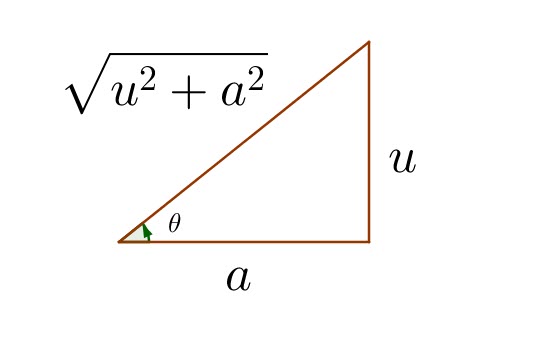
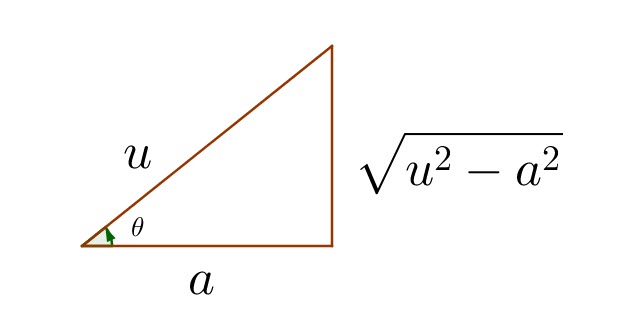
Problem 19
Evaluate: ![]()
This is the scenario containing ![]()
In this istuation, ![]()
Let ![]()
![]()
![]()
Back to the equation:
(1) 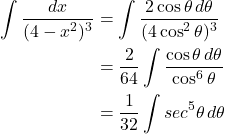
Now let’s Calculate the following:
![]()
Using our methods learned earlier:
(2) 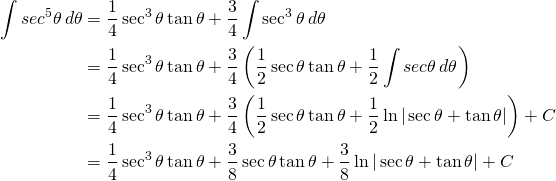
Back to ![]() we should apply the following:
we should apply the following:
![]()
![]()
![]()
![]()
![]()
Let’s apply to the general result:
![]()
(3) 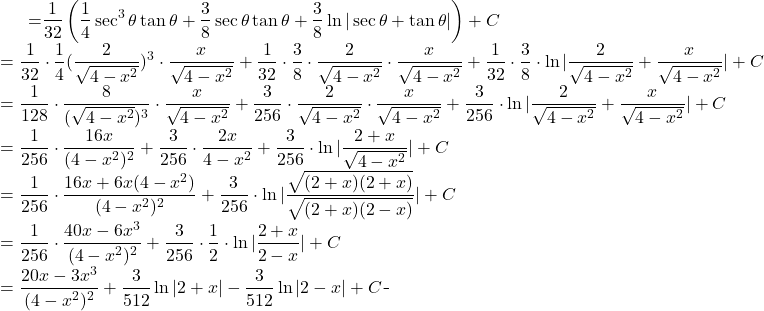
Finally:
![]()
Problem 20
Evaluate: ![]()
This is the scenario containing ![]()
In this istuation, ![]()
Here ![]()
Let ![]()
![]()
![]()
Back to the equation
![]()
Now back to ![]()
![]()
![]()
![]()
(4) 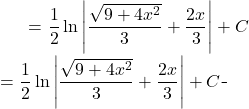
Finally:
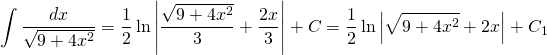
OR:
![]()
By simply using the following hyperbolic substitutions:
Here ![]()
Let ![]()
We get ![]()
![]()
We substitute:
(5) 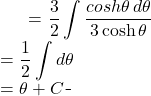
But we have seen that:
![]()
Hence:
![]()
Problem 21
Evaluate: ![]()
This is the scenario containing ![]()
In this istuation, ![]()
Here ![]()
Let ![]()
![]()
![]()
Back to the equation
(6) 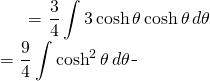
But we know that:
![]()
![]()
(7) 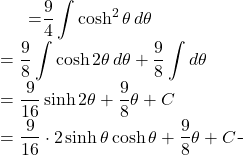
Now getting back to ![]()
![]()
![]()
To our original equation:
(8) ![]()
![]()
Finally:
![]()
OR:
![]()
Problem 22
Evaluate: ![]()
Using trigonmetric substitution
This is the scenario containing ![]()
In this istuation, ![]()
Here ![]()
Let ![]()
![]()
![]()
![]()
![]()
Back to the equation
(9) 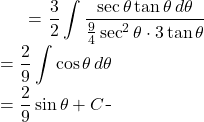
![]()
![]()
Now our equation becomes:
![]()
Finally:
![]()
Problem 23
Evaluate: ![]()
Using hyperbolic substitution
This is the scenario containing ![]()
In this istuation, ![]()
Here ![]()
Let ![]()
![]()
![]()
![]()
![]()
Back to the equation
(10) 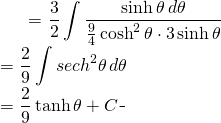
![]()
![]()
![]()
![]()
Back to the original equation:
![]()
Finally:
![]()


Be the first to comment