4.Integration with quadratics in denominator
This is the form:
![]()
Let’s refresh ourselves with these important formulas we saw earlier:
Please note that all these are shown in videos.
![]()
![]()
In previous problems we also discovered the following:
![]()
![]()
We will need these two formulas in this situation.
![]() can be converted to one of the forms :
can be converted to one of the forms :
![]() OR
OR ![]() depending on the sign of
depending on the sign of ![]()
That will allow us to use one of these formulas.
Problem 24
Evaluate:
![]()
We can take care of the quadratic:
![]()
We apply our formula:
(1) 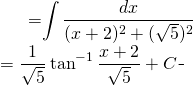
Finally:
![]()
Problem 25
Evaluate:
![]()
We can re-write:
![]()
Let:
![]()
![]()
Back to ![]()
![]()
Finally:
![]()
Problem 26
Evaluate:
![]()
We can re-write:
![]()
Let:
![]()
![]()
Back to ![]()
![]()
Finally:
![]()
Problem 27
Evaluate: ![]()
This is the scenario containing ![]()
In this istuation, ![]()
Here ![]()
Let ![]()
![]()
![]()
Back to the equation
(2) 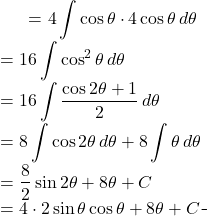
But we know that:
![]()
![]()
![]()
Back to our original equation:
(3) 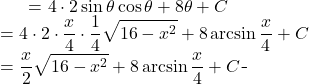
Finally:
![]()


Be the first to comment