5. Partial fractions and rational functions
The rational functions we will integrate must have the coefficient of the numerator less than the one of the denominator.
In addition to that condition, if we can factor the denominator, we will have the partial fractions.
![]()
It may happen that if we consider that ![]() ,
,
the ratio becomes:
![]()
This is the linear Factor of Partial Fractions
We will need to remember the following integration formulas:
![]()
![]() with
with ![]()
Problem 28
Evaluate:
![]()
Let’s factor the denominator:
![]()
![]()
![]()
For ![]()
![]()
For ![]()
![]()
Back to the ratio:
![]()
Back to the evaluation:
(1) 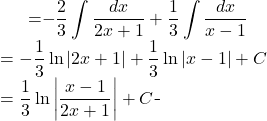
Finally:
![Rendered by QuickLaTeX.com {\displaystyle \int \frac{dx}{2x^{2}-x-1} }={\displaystyle \frac{1}{3} \ln \left | \frac{x-1}{2x+1} \right |+C}={\displaystyle \ln \left |\sqrt[3]{ \frac{x-1}{2x+1}} \right |+C}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-195e1e5bae624917f520b2100dbe1428_l3.png)
Problem 29
Evaluate:
![]()
Let’s factor the denominator:
![]()
![]()
![]()
If ![]()
![]()
If ![]()
![]()
![]()
Back to the ratio:
![]()
Back to the evaluation:
(2) 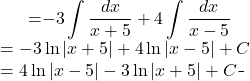
Finally:
![]()
Problem 30
Evaluate:
![]()
Let’s factor the denominator:
![]()
![]()
If ![]()
![]()
![]()
When we plug in:
![]()
The terms in ![]()
![]()
Back to the ratio:
![]()
Back to the evaluation:
(3) 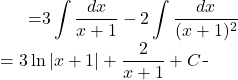
Finally:
![]()
Problem 31
Evaluate:
![]()
Let’s factor the denominator:
![]()
We can get both sides the common denominator of ![]() :
:
We get the following:
![]()
Let ![]()
Only the factor in ![]() will matter:
will matter:
![]()
This yields:
![]()
Now Let ![]()
Only the factor in ![]() will matter:
will matter:
![]()
This yields:
![]()
Now let’s replace plug in ![]() and
and ![]() in the following:
in the following:
![]()
![]()
![]()
![]()
![]()
There is no term in ![]() :
:
We get:
![]()
We pull: ![]()
We can now take the terms in ![]() :
:
![]()
But ![]()
![]()
![]()
![]()
![]()
Hence ![]()
Please note that this verify the constants too: ![]() is true.
is true.
Now back to the ratio:
![]()
![]()
Back to the evaluation:
(4) 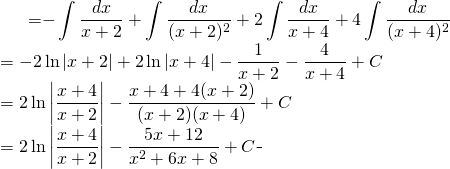
Finally:
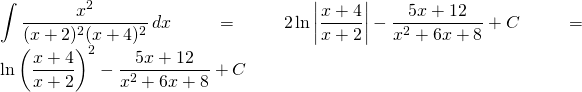
Problem 32
Evaluate:
![]()
Let’s factor the denominator:
![]()
We can now have:
![]()
We can get both sides the common denominator of ![]() :
:
We get the following:
![]()
Let ![]()
Only the factor in ![]() will matter:
will matter:
![]()
This yields:
![]()
Back to the equation:
![]()
![]()
For the terms in ![]()
![]()
![]()
For the constants:
![]()
![]()
You can check this with the xcoefficients in ![]() .
.
Now back to the ratio:
![]()
Back to the evaluation:
![]()
We know that:
![]()
From ![]()
![]()
we also have:
![]()
(5) 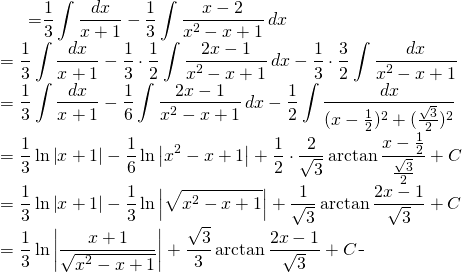
Finally:
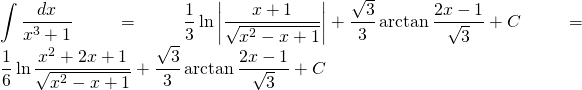
Problem 33
Evaluate: ![]()
This is problem 19 but using partial fractions instead of trigonometric substitution.
First we know that:
![]()
Let’s factor the denominator:
![]()
We can get both sides the common denominator of ![]() :
:
We get the following:
![]()
Let ![]()
Only the factor in ![]() will matter:
will matter:
![]()
Let ![]()
Only the factor in ![]() will matter:
will matter:
![]()
Back to the equation:
![]()
We expand:
![]()
![]()
![]()
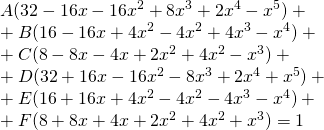
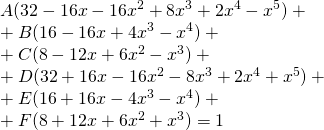
For the terms in ![]()
![]()
For the terms in ![]()
![]()
For the terms in ![]()
![]()
But ![]() and
and ![]()
![]()
![]()
For the terms in ![]()
![]()
Since ![]()
![]()
But ![]()
![]()
![]()
But we have seen above that ![]()
This yields:
![]()
![]()
To summarize:
![]()
![]()
![]()
![]()
![]()
![]()
Now back to the ratio:
![]()
Back to the evaluation:
(6) 
Finally:
![]()


Be the first to comment