6. Integration of irrational functions
Irrational functions are little harder to integrate. There are cases that need some specfic techniques in or order to be integrated.
The method used will depend on the contents of the integrand. We have already used most of these techniques and this part is a kind of summary plus some additions.
case 1: Exponents with fractions
This is the case where we have multiple irrationals combined by the regular operations:
Problem 34
Evaluate: ![]()
We have to re-write using exponents:
![]()
We have to find the commun denominator of all the fractions in exponents.
In this case we have only 2 fractions ![]() and
and ![]()
The common denominator is 4 here.
Let ![]()
![]()
![]()
![]()
Now we get
![]()
When we divide it:
![]()
![]()
![]()
![]()
Now back to ![]() :
:
![]()
Finally:
![]()
Problem 35
Evaluate: ![]()
We have to re-write using exponents:
![]()
The fractions are: ![]() ,
, ![]() and
and ![]()
The common denominator is the LCM of 6 and 4. It is 12.
Let ![]()
![]()
![]()
![]()
Let:
![]()
![]()
For ![]()
![]()
The terms ![]()
![]()
![]()
![]()
The terms in ![]() :
:
![]()
![]()
![]()
![]()
The terms in ![]()
![]()
![]()
![]()
We can now write:
![]()
(1) 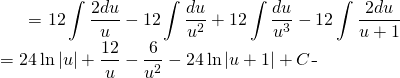
Back to ![]()
We know that ![]()
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{\sqrt[6]{x}+1}{\sqrt[6]{x^{7}}+\sqrt[4]{x^{5}}} \, dx}&= {\displaystyle 24 \ln \left | x^{\frac{1}{12}} \right |+\frac{12}{x^{\frac{1}{12}}}-\frac{6}{(x^{\frac{1}{12}})^{2}}-24 \ln \left |x^{\frac{1}{12}}+1 \right | +C}\\ &= {\displaystyle 24 \ln \left |\sqrt[12]{x} \right |+\frac{12}{\sqrt[12]{x}}-\frac{6}{\sqrt[6]{x}}-24 \ln \left |\sqrt[12]{x}+1 \right | +C} \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-7de1626a98335b66b6bea3dd7a0937da_l3.png)
Finally:
![]()
OR
![]()
case 2: A single fraction with an exponent as fraction
![]()
In this situation we have to use the relation:
![]()
Problem 36
Evaluate: ![]()
Let ![]()
![]()
![]()
![]()
![]()
![]()
We get:
(3) 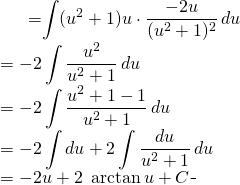
Bax to ![]()
![]()
Finally:
![]()
Problem 37
Evaluate: ![]()
Let ![]()
![]()
![]()
We get:
(4) 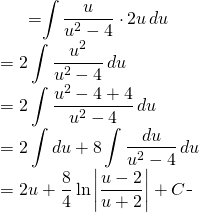
Bax to ![]()
![]()
Finally:
![]()
case 3: Irrational functions in denominator with polynomials in numerator
This form has been solved already :
The form is:
![]()
Problem 38
Evaluate: ![]()
We know that:
![]()
Also:
![]()
![]()
From ![]()
![]()
Back to the evaluation:
(5) 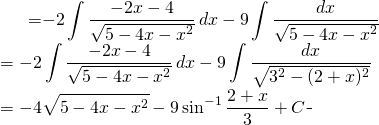
Finally:
![]()
case 4:Other irrational forms
For integrands containing ![]() ,
,![]() or
or ![]()
We have seen above that:
For ![]() , we have the trigonometric substitution with
, we have the trigonometric substitution with ![]() OR
OR ![]()
For ![]() , we have the trigonometric substitution with
, we have the trigonometric substitution with ![]() OR
OR ![]()
For ![]() , we have the trigonometric substitution with
, we have the trigonometric substitution with ![]() OR
OR ![]()
For the form:
![]()
Use:
![]()
In case the quadratic has roots and can be factored:
![]() , we can use
, we can use ![]()
If ![]()
![]() , we can use
, we can use ![]()


Be the first to comment