7. Trigonometric and hyperbolic integrals
Since this site is heavily invested in trigonmetry, we will not come back to formulas we have already seen in the trigometry field.
We’ll focus on some techniques used to integrate trigonometric and hyperbolic functions.
We have already used some of these.
Cases involving 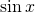 and
and 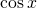
We use the following:
![]()
We can easily show that:
![]()
![]()
![]()
![]()
And with are back to normal rational integration.
Cases of form ![]()
-If ![]() is ODD, use
is ODD, use ![]() .
.
-If ![]() is ODD, use
is ODD, use ![]() .
.
Cases of form ![]()
-If ![]() is ODD, use
is ODD, use ![]() .
.
-If ![]() is EVEN, use
is EVEN, use ![]() .
.
Problem 39
Evaluate: ![]()
we can see that:
![]()
Let ![]()
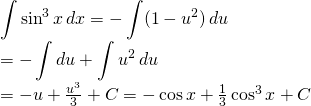
Finally:
![]()
Problem 40
Evaluate: ![]()
We’ll use integration by parts:
Let ![]()
![]()
We get:
![]()
Let:
![]()
We use trigonometric substitution:
Let ![]()
![]()
![]()
(1) 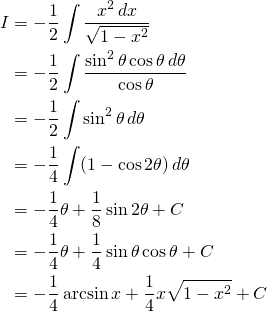
Back to the original:
![]()
![]()
Finally:
![]()
Problem 41
Evaluate: ![]()
![]()
![]()
![]()
Let’s make this integrand easy to compute:
(2) 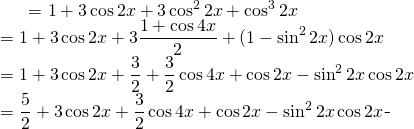
Back to the Equation:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \cos^{6} x \, dx }&={\displaystyle \frac{1}{8} \int (1+\cos 2x)^{3} \, dx }\\ &={\displaystyle \frac{1}{8} \cdot \frac{5}{2} \int dx+\frac{1}{8} \cdot 4 \int \cos 2x \,dx+ \frac{1}{8} \cdot \frac{3}{2} \int \cos 4x \,dx- \frac{1}{16} \int 2\sin^{2} 2x \cos 2x \,dx }\\ &={\displaystyle \frac{5}{16} x+ \frac{4}{16} \sin 2x+ \frac{3}{64} \sin 4x-\frac{1}{48}\sin^{3} 2x+ C}\\ &={\displaystyle \frac{1}{16} \left [ 5x+ 4\sin 2x+ \frac{3}{4} \sin 4x-\frac{1}{3}\sin^{3} 2x \right ]+ C} \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-33fae853359292ed4baade01407e104f_l3.png)
Finally:
![]()
Problem 42
Evaluate: ![]()
![]()
![]()
![]()
We take:
![]()
Let:
![]()
![]()
![]()
![]()
![]()
Now
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Back to the angle
![]()
![]()


Be the first to comment