
Introduction aux matrices
Avant de commencer la résolution des équations, je vais rapidement introduire le calcul matriciel.
Les tables peuvent à tout moment être représentées sous forme de matrice.
On peut dire qu’une matrice est une forme de tableau de nombres.
Les dimensions d’une matrice sont le nombre de ses lignes et de ses colonnes. Une matrice ayant 3 lignes et 5 colonnes se dit une matrice de dimensions ![]() ou “3 sur 5”
ou “3 sur 5”
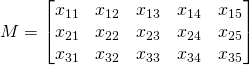
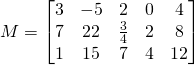
Ou
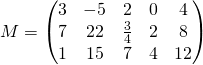
Ou une autre notation:
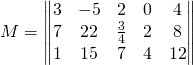
Ou aussi:
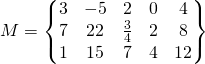
Toutes ces formes peuvent s’utiliser. Nous utiliserons la forme 1 dans la plupart des cas.
Les nombres contenus dans une matrice sont appelés ![]() . Chaque élément a sa propre adresse
. Chaque élément a sa propre adresse
Comme dans le cas des tableurs excel, un élément denote l’intersection d’une ligne et d’une colonne.
Si nous prenons l’élément à la troisième ligne et seconde colonne, nous aurons 15
Nous pouvons l’appeler ![]()
Comparaison de matrices:
Deux matrices sont égales lorsque ces matrices ont la même dimension avec des éléments correspondants qui sont égaux.
Operations sur les matrices:
Addition et soustraction: Quand deux matrices ont la même dimension, nous pouvons les additionner ou les soustraire en additionnant ou en soustrayant les éléments correspondant.
Si nous prenons les matrices suivantes:
![]()
![]()
Nous pouvons les additionner ou prendre leur différence par le fait que ces matrices sont de la même dimension ![]()
![]()
![]()
Pour la soustraction:
![]()
![]()
Multiplication Scalaire:
Pour multiplier une matrice par un nombre, on multiplie chaque élément par ce nombre:
![]()
![]()
-Si nous multiplions une ![]() par un nombre
par un nombre ![]() , tous les éléments doivent être multipliés par ce nombre.
, tous les éléments doivent être multipliés par ce nombre.
Si ![]() , la multiplication donne
, la multiplication donne ![]() de la matrice originale.
de la matrice originale.
![]()
Propriétés:
Les propriétés algébriques s’appliquent à l’addition des matrices:
-Commutativité: ![]()
-Elément neutre : La matrice ![]() ayant seulement
ayant seulement ![]() comme éléments est la matrice neutre pour l’addition.
comme éléments est la matrice neutre pour l’addition.
-Associativité ![]()
-En fin, l’opposé a tous ses éléments qui sont l’opposé des éléments correspondants de ![]()
Multiplication de matrices
Pour que la multiplication soit possible nous devons avoir les conditions suivantes:
Le nombre de colonnes de la matrice de gauche doit être égal au nombre de lignes de la matrice de droite.
La matrice produit a le même nombre de lignes que la matrice à gauche et le même nombre de colonnes que la matrice à droite.
Si ![]() et
et ![]() , pour qu’il y ait multiplication il faut que
, pour qu’il y ait multiplication il faut que ![]()
Après la multiplication: ![]() aura pour dimensions
aura pour dimensions ![]()
Processus: Pour trouver un élément de ![]() en ligne
en ligne ![]() et colonne
et colonne ![]() of
of ![]() , nous devons prendre la somme des produits des éléments correspondant en ligne
, nous devons prendre la somme des produits des éléments correspondant en ligne ![]() de
de ![]() et colonne
et colonne ![]() de
de ![]()
Exemple:
![]()
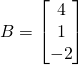
Dans ce cas :
![]() is a
is a ![]() matrix.
matrix.
![]() is a
is a ![]() matrix
matrix
La matrice produit ![]() =
=![]() est une matrice de dimensions
est une matrice de dimensions ![]() .
.
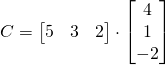
![]()
![]()
Un autre exemple
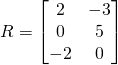
![]()
![]() est une matrice de dimensions
est une matrice de dimensions ![]() .
.
![]() est une matrice de dimensions
est une matrice de dimensions ![]() .
.
La matrice produit ![]() =
=![]() est une matrice
est une matrice ![]() .
.
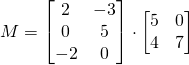
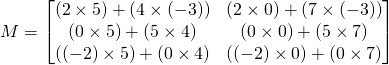
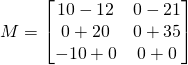
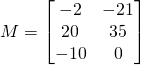
Pour des matrices de plus grande dimension
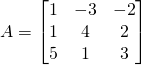
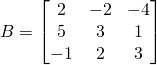
![]() est une matrice
est une matrice ![]() .
.
![]() est une matrice
est une matrice ![]() .
.
La matrice produit ![]() =
=![]() est une matrice
est une matrice ![]() .
.
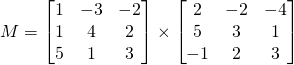
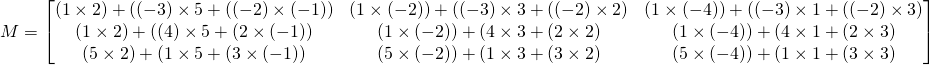
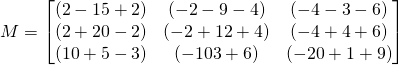
En fin:
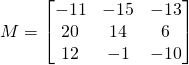
Dans une matrice ![]() , chaque élément est
, chaque élément est ![]() avec
avec ![]() la ligne de l’élément et
la ligne de l’élément et ![]() la colonne de l’élément.
la colonne de l’élément.
SOMMAIRE:
Si ![]() et
et ![]() :
:
La Matrice ![]() si et seulement si pour chaque
si et seulement si pour chaque ![]() et
et ![]() ,
, ![]()
La Matrice ![]() Si et seulement si pour chaque
Si et seulement si pour chaque ![]() et
et ![]() ,
, ![]()
L’opposé ![]() de
de ![]() est la matrice
est la matrice ![]()
Le produit d’un nombre réel ![]() et d’une matrice
et d’une matrice ![]() vaut
vaut ![]()
Lorsque la multiplication peut avoir lieu, ![]() matrice produit de
matrice produit de ![]() et de
et de ![]() a les éléments
a les éléments ![]()
Matrices importantes
Matlab se base beaucoup sur le calcul matriciel. C’est important de savoir l’existence de certains types de matrices.
Matrice Carrée
Le nombre de lignes vaut le nombre de colonnes dans ce type de matrices
Si ![]() est une matrice
est une matrice ![]() , on l’appelle
, on l’appelle ![]() .
.
Dans ce cas, ![]() est une matrice d’ordre
est une matrice d’ordre ![]() .
.
Les éléments de la diagonale principale de ![]() sont
sont ![]()
Matrice Identité
Matrice qui se note ![]() est une matrice d’ordre
est une matrice d’ordre ![]() avec chaque élément de la diagonale principale qui vaut
avec chaque élément de la diagonale principale qui vaut ![]() et tous les autres éléments valent
et tous les autres éléments valent ![]() .
.
Exemples
![]()
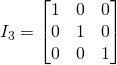
Nous pouvons noter que:
![]()
Matrice Inverse
L’inverse de la matrice ![]() d’ordre
d’ordre ![]() que l’on désigne
que l’on désigne ![]() , appelé
, appelé ![]() est telle que:
est telle que: ![]()
Certaines matrices n’ont pas d’inverse.
Trouver l’inverse sans utiliser les ![]() est long.
est long.
Des vidéos sont prévues à cet effet.
En résolvant l’équation ![]() , on trouve
, on trouve ![]()
Exemple:
![]()
Et
![]()
Nous avons
![]()
Mais ![]() puisque
puisque ![]() est d’ordre 2.
est d’ordre 2.
Nous avons
![]()
![]()
![]()
![]()
![]()
Nous trouvons:
![]()
Enfin:
![]()
Matrice Transposée:
La transposée de ![]() que l’on note
que l’on note ![]() est une nouvelles matrice dont les colonnes sont les lignes de
est une nouvelles matrice dont les colonnes sont les lignes de ![]() et dont les lignes sont les colonnes de
et dont les lignes sont les colonnes de ![]() .
.
Si nous avons:
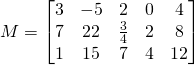
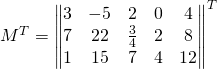
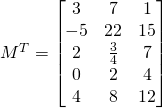
Nous remarquons que:
![]() est une matrice
est une matrice ![]() et
et
![]() est une matrice
est une matrice ![]() .
.
On peut dire que:
If ![]()
Aussi noter que:
![]()
Déterminants:
Toute matrice carrée est associée à un déterminant.
Une matrice est inversible si et seulement si son déterminant est différent de 0.
Pour une matrice ![]() ,
,
Le déterminant est ![]()
A ne pas confondre avec la ![]() de
de ![]() .
.
Dans certains documents le déterminant est écrit ![]() pour éviter toute confusion.
pour éviter toute confusion.
Matrice d’ordre 1
C’est une matrice avec un seul élément.
![]()
Le déterminant de ![]() est :
est :
![]()
Matrice d’ordre 2
Ce type de matrice carrée est une matrice ![]() .
.
![]()
![]()
![]()
Exemple:
![]()
Le déterminant:
![]()
![]()
Mineurs and Cofacteurs:
Pour une matrice carrée d’un ordre ![]() , nous utiliserons les mineurs et cofacteurs pour calculer le déterminant:
, nous utiliserons les mineurs et cofacteurs pour calculer le déterminant:
Si ![]() est une matrice carrée d’ordre
est une matrice carrée d’ordre ![]() ,
,
Le ![]()
![]() de l’élément
de l’élément ![]() est le déterminant de la matrice d’ordre
est le déterminant de la matrice d’ordre ![]() avec le ligne
avec le ligne ![]() et la colonne
et la colonne ![]() effacées.
effacées.
Le ![]()
![]() is
is ![]()
Le déterminant de ![]() d’ordrer
d’ordrer ![]() se calcule comme suit:
se calcule comme suit:
-Lexpansion du cofacteur d’une ligne donnée (Choisir la ligne contenant le plus de ![]() pour accélérer les calculs:
pour accélérer les calculs:
![]() . Par la ligne 1 ici.
. Par la ligne 1 ici.
Ou par les mineurs:
![]()
Exemple:
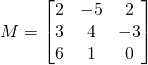
Utilisons la ligne 3 qui contient un ![]()
![]()
![]()
![]()
![]()
Enfin:
![]()
Transformations des lignes d’une matrice
On peut transformer une matrice originale en effectuant une ou toutes les operations suivantes:
– En interchangeant deux lignes.
-En multipliant une ligne par un facteur ![]()
– En multipliant ou divisant une ligne par un facteur ![]() et en ajoutant le résultat obtenu à une autre ligne pour la changer.
et en ajoutant le résultat obtenu à une autre ligne pour la changer.
Prenons le système d’équations suivant:
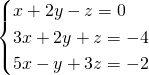
Ecrivons la matrice augmentée:
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 3 &2 & 1 &-4 \\ 5 & -1 & 3 & -2 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-ba7b4e4ad520218be61a7ad904ff3fe8_l3.png)
Pour la nouvelle ligne 2, multiplions la ligne 1 par ![]() et ajoutons à la ligne 2. Le résultat devient la nouvelle ligne 2.
et ajoutons à la ligne 2. Le résultat devient la nouvelle ligne 2.
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 0 &-4 & 4 &-4 \\ 5 & -1 & 3 & -2 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-defc62c4303720f183e69beabbbd39bb_l3.png)
Pour cette étape, divisons la ligne 2 par ![]()
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 0 &1 & -1 &1 \\ 5 & -1 & 3 & -2 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-bb3dd0e50076c20c4a847972a310c0ce_l3.png)
Multiplions maintenant la ligne 1 par ![]() et ajoutons à la ligne 3. Le résultat devient la nouvelle ligne 3.
et ajoutons à la ligne 3. Le résultat devient la nouvelle ligne 3.
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 0 &1 & -1 &1 \\ 0 & -11 & 8 & -2 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-c03e5f8ed6c3269b5157c11eb385bba4_l3.png)
Multiplions maintenant la ligne 2 par ![]() et ajoutons à la ligne 3. Le résultat devient la nouvelle ligne 3.
et ajoutons à la ligne 3. Le résultat devient la nouvelle ligne 3.
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 0 &1 & -1 &1 \\ 0 & 0 & -3 & 9 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-8515ed7dd8e5cf54c21c536103c4a6af_l3.png)
On peut maintenant écrire:
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 3 &2 & 1 &-4 \\ 5 & -1 & 3 & -2 \\ \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-ba7b4e4ad520218be61a7ad904ff3fe8_l3.png) =
=![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc|c} 1 & 2 & -1 & 0 \\ 0 &1 & -1 &1 \\ 0 & 0 & 1 & -3 \\ \end{array} \right] \Rightarrow \begin{cases} x+2y- z= 0\\3x+2y+ z=-4\\5x- y+3z=-2 \end{cases}= \begin{cases} x+2y- z= 0\\y- z=-1\\z=-3 \end{cases}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-60401bd21cb4f0fb781f970720078abd_l3.png)
Utilisation de l’inverse 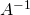 de la matrice
de la matrice 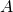
1: Trouver le déterminant ![]() , doit être non-zero.
, doit être non-zero.
2: Trouver la matrice transposée ![]()
3: Trouver la comatrice, avec chaque élément ![]() remplacé par son cofacteur
remplacé par son cofacteur ![]()
4:Trouver la matrice inverse ![]() en divisant la matrice trouver à l’étape 3 par le déterminant
en divisant la matrice trouver à l’étape 3 par le déterminant ![]() trouvé au 1.
trouvé au 1.
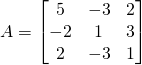
![]()
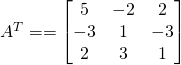
La comatrice :
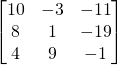
La matrice inverse ![]()
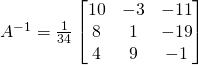
Déterminants: Règle de Sarrus
Pour une matrice de dimension 3 x 3, il existe une règle appelée règle de Sarrus utilisée pour simplifier les calculs des déterminants. Avec cette méthode, on n’a pas besoin de cofacteurs.
D’autres méthodes sont suggérées pour les matrices de dimensions ![]() et d’ordre supérieur. Cependant, dans ce texte, nous allons nous limiter nos calculs aux matrices de dimensions
et d’ordre supérieur. Cependant, dans ce texte, nous allons nous limiter nos calculs aux matrices de dimensions ![]() .
.
Processus:
Nous ajoutons la première colonne comme quatrième colonne et la deuxième colonne comme cinquième colonne.
Si nous avons une matrice:

Le déterminant:
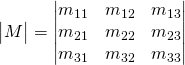
Maintenant nous ajoutons les deux premières colonnes:
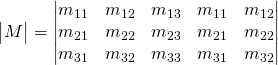
On prend la somme des diagonales descendantes de 3 éléments chacune et l’on soustrait la somme des diagonales ascendantes:


![]()
Résoudre en utilisant la Règle de Sarrus:
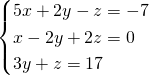
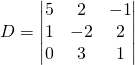

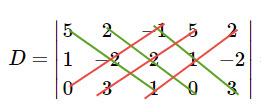
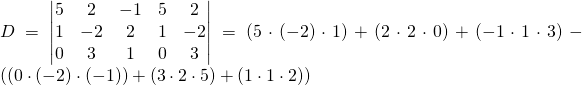
![]()
Maintenant pour ![]()
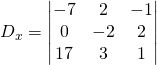
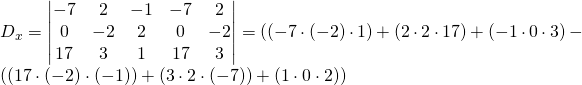
![]()
![]()
Pour ![]()
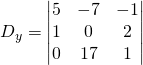
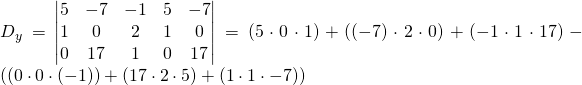
![]()
![]()
Pour ![]()
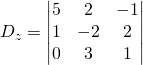
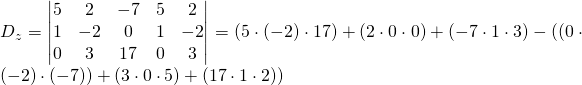
![]()
![]()
En fin, la solution est ![]()
Trouver un nombre xyzuw
Un nombre de 5 chiffres s’écrit xyzuw.
La somme de ses chiffres est de 22.
En changeant l’ordre des chiffres et l’écrivant xywuz, sa valeur est augmentée de 297.
Le chiffre x ajouté au chiffre u et de 2 fois les chiffres y et w, et puis diminué de 3 fois le chiffre z donne 21.
Deux fois le chiffre x ajouté au chiffre z et puis diminué de 3 fois le chiffre y et de 4 fois le chiffre w donne -34
Deux fois le chiffre u diminué du chiffre w et de 3 fois le chiffre z donne -1.
Trouver le nombre xyzuw.
Résolution par substitution:
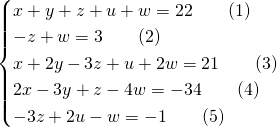
De ![]() nous avons:
nous avons:
![]()
![]()
De ![]() :
:
![]()
En remplaçant ![]() par sa valeur de
par sa valeur de ![]()
![]()
![]()
![]()
![]()
Nous allons diminuer ![]() de
de ![]() :
:
![]()
![]()
![]()
![]()
In ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
En remplaçant toutes ses variables par leur valeur dans ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
En fin:Le nombre recherché est de:
![]()
Video sur la solution par substitution
Utilisation de la Matrice inverse:
Nous avons la matrice augmentée:
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\1 & 2 & -3 & 1&2&21\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & -3 & 2&-1&-1 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-880a5e0d2b5b42edab03e6dadb783e5b_l3.png)
En prenant ![]()
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\0 & 1 & -4 & 0&1&-1\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & -3 & 2&-1&-1 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-9a869eadbe6688593ec3128a52d47de3_l3.png)
En prenant ![]()
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\0 & 1 & -4 & 0&1&-1\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & 0 & 2&-4&-10 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-fb89073da26691432bf5f34ba6e7608d_l3.png)
Trouver:![]()
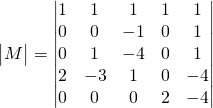
On utilise la ligne 2 qui ne contient que 2 valeurs:![]() se trouvant sur la ligne 2 et la colonne 3,
se trouvant sur la ligne 2 et la colonne 3, ![]() De même que pour 1 (ligne 2 colonne 5).
De même que pour 1 (ligne 2 colonne 5).
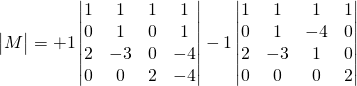
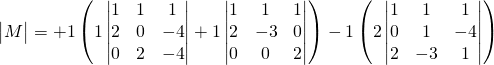
![]()
![]()
Le determinant ![]() , ainsi la matrice est inversible:
, ainsi la matrice est inversible:
La transposée de ![]() est
est
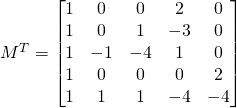
La comatrice a 25 éléments, nous calculerons 2 éléments, le reste pourra être calculé comme exercice.
Pour ![]() de la comatrice:
de la comatrice:
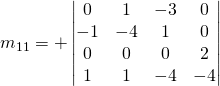
![]()
Pour ![]() de la comatrice:
de la comatrice:
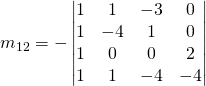
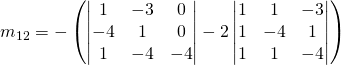
![]()
![]()
Finalement nous avons:
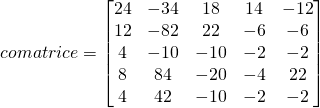
La matrice ![]() est de:
est de:
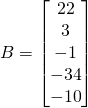
La solution est de:
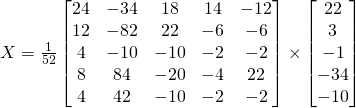
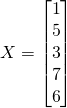
Cramer’s rule
Nous avions preparé la solution en haut et avons trouvé un système d’équations simple.
Comme pratique il faut calculer les matrices suivantes:
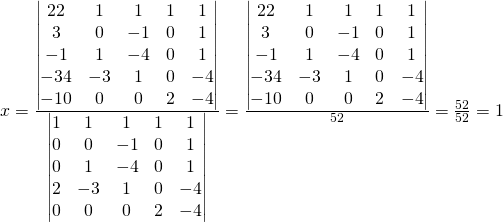
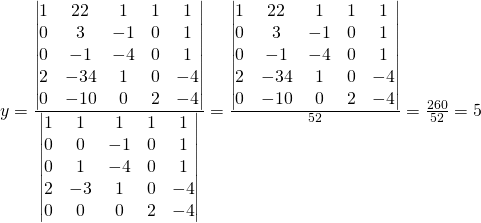
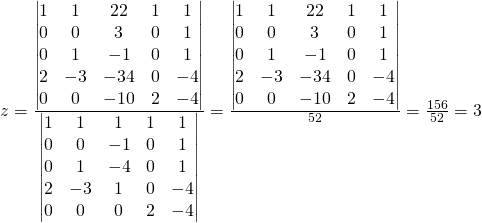
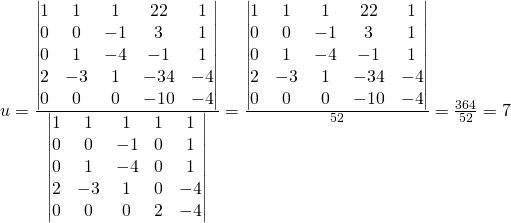
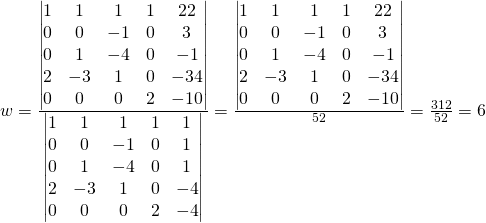
Calculer: ![]()



Be the first to comment