Introduction aux nombres complexes
Les nombres complexes sont des nombres sous la forme ![]() .
.
Ces nombres sont largement utilisés pour trouver des solutions rapides dans des domaines comme Electricité, navigation, etc…
Sous cette forme, ![]() et
et ![]() sont des réels. L’unité
sont des réels. L’unité ![]() est l’unité imaginaire. On notera que
est l’unité imaginaire. On notera que ![]() .
.
Si nous prenons ![]() ,
, ![]() est la partie réelle et la partie
est la partie réelle et la partie ![]() est la partie imaginaire.
est la partie imaginaire.
Nous voyons que:
![]() and
and ![]()
Autour du 16ème siècle, le besoin de trouver la solution de ![]() est devenu évident.
est devenu évident.
Pour représenter l’image d’un nombre complexe dans le plan complexe, la partie réelle est projetée sur l’axe des ![]() pendant que la partie imaginaire sera projetée sur l’axe des
pendant que la partie imaginaire sera projetée sur l’axe des ![]()
Les règles concernant les quadrants restent les mêmes.
Un imaginaire pur est de la forme ![]() avec
avec ![]() un nombre réel.
un nombre réel.
![]()
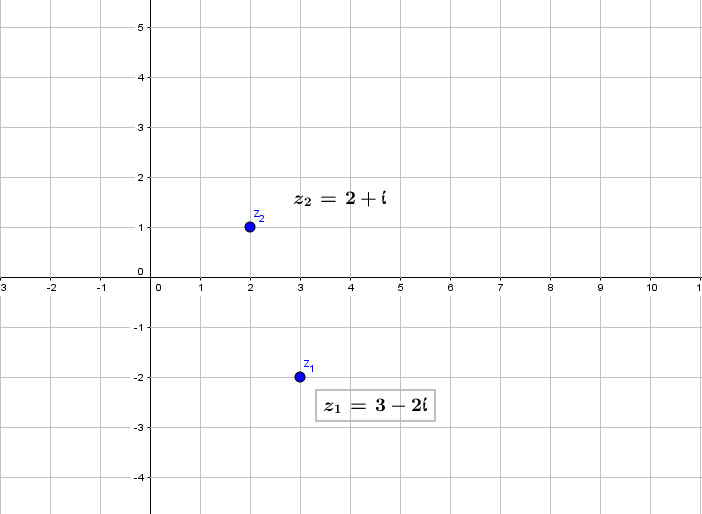
Quand un nombre complexe a deux composantes, on le représente sur le plan des complexes. C’est le ‘Diagramme d’Argand’.
Un point ![]() sera représenté par le complexe
sera représenté par le complexe ![]() .
.
Nous appelons l’axe des ![]() , l’axe des
, l’axe des ![]() et l’axe des
et l’axe des ![]() , l’axe des
, l’axe des ![]() .
.
Un point ![]() peut se représenter par un vecteur aussi. Pour ajouter
peut se représenter par un vecteur aussi. Pour ajouter ![]() à un nombre complexe, on effectue une simple translation par vecteur
à un nombre complexe, on effectue une simple translation par vecteur ![]()
![]() est une translation de
est une translation de ![]() unités vers la droite et
unités vers la droite et ![]() unités en haut dans le plan des complexes.
unités en haut dans le plan des complexes.

Egalité de nombres complexes
Pour que deux nombres complexes:
![]()
Les conditions suivantes devront être remplies:
![]() and
and ![]()
Exemple1:
![]() signifie que:
signifie que:
![]() et
et ![]()
Exemple2:
Trouver ![]() et
et ![]() , les nombres réels dans l’équation suivante:
, les nombres réels dans l’équation suivante:
![]()
Nous avons:
![]() , partie réelle
, partie réelle
![]()
![]()
![]() , partie imaginaire
, partie imaginaire
Finalement:
Réponse: ![]() et
et ![]()
Addition et soustraction de nombres complexes
Pour trouver la somme ou la différence de deux nombres complexes, on ajoute ou on soustrait les parties réelles entre elles et les parties imaginaires entre elles.
![]()
![]()
![]()
Produit de nombres complexes
Si ![]() et
et ![]()
![]()
![]()
Exemple:
![]()
Complexes Conjugués
Si ![]() est un complexe, son conjugué se note
est un complexe, son conjugué se note ![]()
Voir la figure suivante:

On peut aussi noter que:![]()
Si nous prenons l’équation quadratique avec ![]() , avec 2 racines complexes, on peut voir que ces deux racines constituent deux nombres complexes conjugués
, avec 2 racines complexes, on peut voir que ces deux racines constituent deux nombres complexes conjugués
Propriétés des conjugués:
La somme et le produit de deux complexes conjugués donnent un nombre réel dans chacun des cas.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exemples:
![]()
![]()
Quotients de deux nombres complexes
Pour rationaliser cette expression, on multiplie le complexe au dénominateur par son conjugué.
Nous avons: ![]()
![]()
Ce qui donne:![]()
Important:
Pour des complexes ![]() et
et ![]() :
:
![]()
![]()
Si le complexe ![]() , nous aurons:
, nous aurons:
![]()
Mettre sous forme ![]() :
:
![]()
Solution:
![]()
Equations quadratiques
Trouver ![]() dans
dans ![]()
![]()
On peut dire:![]()
Nous savons que:![]()
On obtient
![]()
Racine 1: ![]()
On trouve maintenant la solution de:
![]()
Nous avons:![]()
Cependant: ![]()
Ce qui signifie![]()
![]()
![]()
La Racine 3 est le complexe conjugué:
![]()
En fin:
Réponse: ![]() ,
, ![]() and
and ![]()


Be the first to comment