Introduction aux vecteurs et coordonnées polaires
Vectors:
Les vecteurs trouvent leur utilisation dans les domaines de la navigation, de la physique, ingénierie, etc…
Le vecteur est toujours défini par sa longueur ou magnitude et par sa direction.
En prenant l’exemple d’un navire qui suit un certain cap avec une certaine vitesse, on utilise les vecteurs pour calculer les points d’approche d’autres cibles.
Sans la direction, la magnitude n’est qu’un scalaire.
Les vecteurs se notent avec des lettres miniscules comme ![]() ou
ou ![]() .
.
Ils peuvent aussi se noter ![]() . la longueur sera alors de
. la longueur sera alors de ![]() ou
ou ![]()
Pour vecteur ![]() , la longueur peut se noter
, la longueur peut se noter ![]() .
.
L’addition des vecteurs peut se faire avec les angles et magnitudes ou simplement par graphique.
Loin de se reclamer un cours sur les vecteurs, ce petit rappel nous sera utile pour le sujet en cours.
Coordonnées polaires 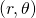
Sur le plan ce sont::![]() qui est la distance de l’origine et
qui est la distance de l’origine et ![]() un angle entre
un angle entre ![]() and
and ![]() . Le sens est le sens trigonométrique ou direct ou contraires des aiguilles d’une montre.
. Le sens est le sens trigonométrique ou direct ou contraires des aiguilles d’une montre.
![]() .
.
Il faut noter que:
![]()
Polaire et Cartésien
Pour un ![]() , nous avons
, nous avons ![]()
Nous voyons clairement les relations trigonométriques![]()
![]()
Elevant les 2 membres au carré:
![]()
On peut aussi diviser:
![]()
Expression utile dans les calculs complexes.
Module d’un nombre complexe
Le ![]() d’un nombre complexe
d’un nombre complexe ![]() qui se note
qui se note ![]() est la distance de l’origine au point Z.
est la distance de l’origine au point Z.
C’est aussi la longueur du vecteur qui correspond au complexe ![]()
Pour tout complexe nous avons:![]() . La distance est toujours
. La distance est toujours ![]() .
.

Ce qui donne:
![]()
On peut écrire la même équation:
![]()
Autres formules:
![]()
![]()
![]() if
if ![]()
Argument d’un nombre complexe
L’argument du complexe ![]() est l’angle
est l’angle ![]() entre laxe des réels et la droite joignant
entre laxe des réels et la droite joignant ![]() to
to ![]() .
.
C’est ![]() .
.

Coordonnées polaires d’un nombre complexe:
Nous venons de voir le module et l’argument d’un nombre complexe. Ces données sont très utiles dans les calculs des complexes.
Soit: ![]() and
and ![]() .
.
On a:
![]() and
and ![]()
Maintenant ![]() is:
is:
![]()
En factorisant:
![]()
On voit clairement que l’on utilisera des multiples de ![]() , donnant de multiples valeurs de Arg(z).
, donnant de multiples valeurs de Arg(z).
Pour éviter cette situation on définit une valeur principale pour ![]() dans l’intervalle
dans l’intervalle ![]()
Pour tout complexe ![]() on aura:
on aura:
![]()
Calculer 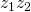 avec les coordonnées polaires
avec les coordonnées polaires
![]()
![]()

Ceci montre que le nouveau module est le produit des modules et que le nouvel arg(z) est la somme des arguments.
On rencontre des fois la notation:
![]()


Be the first to comment