Introduction aux nombres complexes

Formule d’Euler

Puissances de 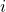$i$

$i^0=1$
$i^1=i$
$i^2=-1$
$i^3=-i$
$i^4=1$
$i^5=i$

En conlusion:

Si $n$ est pair et $n=2k$ , nous aurons $i^n=i^{2k}=(i^2)^k=(-1)^k$
Si $n$ est impair $n=2k+1$ , nous avons $i^n=i^{2k}\cdot i=(i^2)^k=(-1)^k\cdot i$

Exemple:
$i^{203}$ Nous pouvons dire que $n=2k+1=203 \Rightarrow 2k=202$ avec $k=101$ .
Nous avons: $i^{203}=(-1)^{101}\cdot i=-i$

La formule d’Euler sert à représenter les coordonnées polaires.

$\cos \theta+ \sin \theta i=e^{\theta i}$

Qui se simplifie en:

$e^{z_1+z_2}=e^{z_1}\cdot e^{z_2}$

$e^{z_1z_2}=(e^{z_1})^{z_2}$

Lorsque $r>0$ nous aurons:

$z=r\cdot e^{\theta i}$

On aura aussi:

$z_1z_2=r_1r_2e^{(\theta_1+\theta_2)i}$

Si $z=x+iy$ On peut écrire:

$e^{z}=e^{x}e^{iy}$

Exemple:

$e^{i\pi}=-1$

$e^{i\frac{\pi}{2}}=i$

Les formules d’Euler:

$\cos (\theta)=\frac{e^{i\theta}+e^{-i\theta}}{2}$

$\sin (\theta)=\frac{e^{i\theta}-e^{-i\theta}}{2i}$

Formule de Moivre

Si $n$ est un entier positif,alors

$(\cos \theta+i\sin \theta)^{n}=\cos n\theta+i\sin n\theta$

Si nous avons:

$z=r(\cos \theta+i\sin \theta)$

Alors:

$z^n=r^n(\cos n\theta+i\sin n\theta)$

Exemple: $z^n=1$

Cette équation aura $n$ racines distinctes:

$\mathbb{C}_k=e^{\frac{2k\pi i}{n}}$ avec $k=0,1, \cdots, n-1$

Ces racines sont équitablement positionnées sur le cercle de rayon 1.

Pour:

$z^n=a$

Soit $\phi$ l’argument $arg(z)$

On a $a=|a|e^{i\phi}$

$z_k=|a|^{\frac{1}{n}}e^{i(\phi+2k\pi)}$

$k=0,1, \cdots, n-1$

Racines d’un nombre complexe

Nous utiliserons la formule de Moivre pour trouver les racines d’un nombre complexe.

Avec $n>0$ étant un réel, noue pouvons trouver les racines $nièmes$ du nombre complexe. Ces racines forment un polygone regulier. Pour un module de $1$ , ces racines sont sur le cercle unitaire. Quand le module est $>0$ , les racines sont sur le cercle de rayon le $module$ .

Nous verrons quelques exemples.

Exemple:

Calculer les racines de:
$z^2=1+i$

Deux méthodes.

Méthode 1:

On prend $z=x+yi$
$z^2=(x+yi)^2$
$z^2=(x+yi)(x+yi)$
$z^2=x^2-y^2+2xyi$

De l’énoncé: $z^2=1+i$

Nous avons:
$x^2-y^2+2xyi=1+i$

Parties réelles sont égales et les parties imaginaires sont égales

Ce qui donne:
$x^2-y^2=1$ et $2xy=1$

De la seconde équation:
$2xy=1 \Rightarrow 4x^2y^2=1$

Mais $x^2-y^2=1 \Rightarrow y^2=x^2-1$

Ce qui donne:
$4x^2(x^2-1)=1$
$4x^4-4x^2=1$
$4x^4-4x^2-1=0$

$\Delta=16+16=32$

$x^2=\frac{4+\sqrt{16\cdot 2}}{8}$
$x^2=\frac{4+4\sqrt{2}}{8}$

$x^2=\frac{1+\sqrt{2}}{2}$ l’autre valeur est $<0$
$x=\pm \sqrt{\frac{1+\sqrt{2}}{2}}$
$2xy=1 \Rightarrow y=\frac{1}{2x}$
$y=\pm \frac{1}{2 \cdot \sqrt{\frac{1+\sqrt{2}}{2}}}$

On peut transformer $y$ :

$y=\pm \frac{1}{\sqrt{2} \cdot \sqrt{1+\sqrt{2}}}$

Finalement notre solution:

Réponse: $z=\pm (\sqrt{\frac{1+\sqrt{2}}{2}}+i\frac{1}{\sqrt{2} \cdot \sqrt{1+\sqrt{2}}})$

Secnde méthode:

$z^2=1+i$

$r=\sqrt{1^2+1^2}$

$r=\sqrt{2}$

$z^2=\sqrt{2}(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i)$

L’argument de base $\theta=\frac{\pi}{4}$

La formule d’Euler:

$z^2=\sqrt{2}e^{i\frac{\pi}{4}}$

Pour les racines:

$z=(\sqrt{2})^{\frac{1}{2}}e^{i(\frac{\frac{\pi}{4}+2k\pi}{2})}$

$z=(\sqrt{2})^{\frac{1}{2}}e^{i(\frac{\pi}{8}+k\pi)}$

Pour $k=0$

$z=\sqrt{\sqrt{2}}e^{i(\frac{\pi}{8})}$

$z=\sqrt{\sqrt{2}}(\cos \frac{\pi}{8}+i \sin \frac{\pi}{8})$

Mais $\frac{\pi}{4}=2\frac{\pi}{8}$

On sait que:
$\cos 2\theta=\cos^{2}\theta-\sin^{2}\theta$

Ce qui signifie:
$\cos \theta=\sqrt{\frac{1+\cos 2\theta}{2}}$
$\sin \theta=\sqrt{\frac{1-\cos 2\theta}{2}}$

Nous savons quet:
$\cos \frac{\pi}{4}=\sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}$
Ce qui donne:
$z=\sqrt{\sqrt{2}}(\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}+i\sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}})$

La partie réelle:
Si nous mettons $r$ sous le radical:
$\sqrt{\sqrt{2}}(\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}})=\sqrt{\frac{2\sqrt{2}+\sqrt{2}\cdot \sqrt{2}}{4}}=\sqrt{\frac{1+\sqrt{2}}{2}}$

La partie imaginaire:

Si nous mettons $r$ sous le radical:

$\sqrt{\sqrt{2}}(\sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}})=\sqrt{\frac{2\sqrt{2}-\sqrt{2}\cdot \sqrt{2}}{4}}=\sqrt{\frac{\sqrt{2}-1}{2}}$

On rationalise:
$\sqrt{\frac{\sqrt{2}-1}{2}}=\sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}+1)}{2(\sqrt{2}+1)}}=\sqrt{\frac{1}{2(\sqrt{2}+1)}}=\frac{1}{\sqrt{2}\sqrt{\sqrt{2}+1}}$