Transformations et nombres complexes
Toute transformation sur le plan d’un point ![]() donne son image
donne son image ![]() .
.
On associe chaque point à son affixe. On appelle ces deux ![]() et
et ![]() , deux nombres complexes.
, deux nombres complexes.
On écrit la transformation en utilisant les nombres complexes:
![]() avec
avec ![]() une fonction complexe qui associe
une fonction complexe qui associe ![]() à
à ![]()
Translation
Pour un vecteur ![]() nous avons un affixe
nous avons un affixe ![]() .
.
On a:
![]()
Une simple addition de deux vecteurs.
Prenons un point ![]() d’affixe
d’affixe ![]()
On fait une translation de ![]() . Simple addition de deux complexes
. Simple addition de deux complexes ![]()
On aura un autre point ![]() qui est l’image de
qui est l’image de ![]() d’affixe
d’affixe ![]()
![]()
![]()
Imaginer un navire qui a une certaine vitesse suivant un cap donné.
Rotation avec les nombres complexes
La rotation doit se centrer à l’origine ![]() . Si
. Si ![]() est l’angle de rotation:
est l’angle de rotation:
L’image de ![]() est
est
![]()
Ce cas est simple. Maintenant prenons un autre centre de rotation ![]() d’affixe
d’affixe ![]() .
.
L’idée sera de ramener le centre au point (0,0). Une simple translation en ajoutant ![]() en premier, on effectue la rotation et enfin on ajoute
en premier, on effectue la rotation et enfin on ajoute ![]() pour compenser la première translation.
pour compenser la première translation.
![]()
Exemple:
Rotation autour 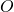
Un point ![]() d’affixe
d’affixe ![]() subit une rotation autour de l’origine d’un angle de
subit une rotation autour de l’origine d’un angle de ![]() , trouver le point
, trouver le point ![]() d’affixe
d’affixe ![]() , image de
, image de![]() après la rotation.
après la rotation.
![]() ,
, ![]() est l’angle de base.
est l’angle de base.
Expression exponentielle:![]()
On utilise la formule de rotation:![]()
![]()
Rotation autour d’un point quelconque
Avec un point ![]() d’affixe
d’affixe ![]() autour d’un autre point
autour d’un autre point ![]() d’affixe
d’affixe ![]() d’un angle de
d’un angle de ![]()
On utilise la formule:![]()
![]()
L’image finale:![]() ,
, ![]() est l’angle de base.
est l’angle de base.![]()
L’image finale



Be the first to comment