Exercices et solutions
Exercise:
![]()
![]()
Trouver ![]() ,
,![]() ,
,![]() and
and ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: Trouver ![]() ,
,![]() ,
,![]() and
and ![]() “]
“]
Solution:
On remarque que ![]()
![]()
![]()
![]()
![]()
En fin:![]()
[/item] [/accordion]
Evaluer:
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
Solution
Let ![]()
Expression polaire:
Le module:![]()
Maintenant pour l’argument:
Si ![]() ,
,
![]()
![]()
Nous voyons que ![]()
Ce qui donne:![]()
Une autre forme:![]()
Avec la formule de Moivre
![]()
![]() Mais:
Mais: ![]()
Maintenant nous avons ![]()
![]()
![]()
![]()
![]()
Finalement:
Réponse: ![]()
[/item] [/accordion]
Problèmes:
Trouver les racines 8ièmes de ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: Trouver les racines 8ièmes de ![]() “]
“]
Solution:
![]() , trouver les 8 racines
, trouver les 8 racines
Soit ![]()
![]()
Module:
![]()
![]()
Forme polaire:
![]()
![]()
![]() de
de ![]() à
à ![]()
Les racines:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalement:
Réponse:![]()
[/item] [/accordion]
Résoudre en ![]()
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour la solution de: ![]() “]
“]
Solution
![]()
![]()
![]()
![]()
![]()
Un défi consiste à trouver un autre nombre complexe, ![]()
Soit ![]()
Le module:
![]()
Maintenant:
![]()
Angle de base:
![]()
Du cercle trigonométrique, sinus et cosinus <0, l’angle est l’angle de base plus 180 degrés.
![]()
Cependant, notre notation ![]() nous donne
nous donne ![]()
Maintenant:
![]()
![]()
![]()
![]()
![]()
![]()
Finalement:
Réponse: ![]()
[/item] [/accordion]
Problèmes:
Résoudre en ![]()
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour trouver la solution de: ![]() “]
“]
Solution
![]()
Soit ![]()
Module:
![]() Noter que
Noter que ![]()
Maintenant arg(w)
![]()
Du cercle trigonométrique:
L’angle de base ici est ![]()
Ce qui donne ![]()
Nous cherchons 3 racines avec ![]()
La notation devient:
![]()
Alors:
![]()
Les racines:
![]()
![]()
![]()
Quelques formules:
![]()
![]()
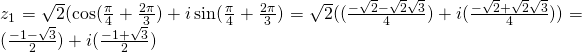
![]()
For ![]() we use the transformation formulas and we get:
we use the transformation formulas and we get:
![]()
![]()

[/item] [/accordion]
Problème:
Evaluer ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
Solution
Deux voies:
Le binôme:
![]()
Notation polaire complexe![]()
Module:![]()
![]()
L’angle de base: ![]() qui est ausi l’argument
qui est ausi l’argument ![]()
![]()
![]()
![]()
![]()
Finalement:
Answer: ![]()
[/item] [/accordion]
Problème:
Evaluer ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
Solution
![]()
Seconde méthode:
![]()
![]()
Angle de base![]()
Avec un ![]() qui est
qui est ![]() , nous sommes au 1er quadrant.
, nous sommes au 1er quadrant.
Alors, ![]()
![]()
![]()
Angle de base![]()
Avec le ![]() qui est
qui est ![]() , 4eme quadrant.
, 4eme quadrant.
Alors, ![]()
Le produit:
![]()
![]()
Answer: ![]()
[/item] [/accordion]
Problème:
Evaluer ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour la solution de: ![]() “]
“]
Solution
Deux méthodes:
Première méthode![]()
L’autre méthode, plus efficace pour beaucoup de complexes.
![]()
![]()
Angle de base![]()
Avec le ![]() qui est
qui est ![]() , nous sommes au premier quadrant.
, nous sommes au premier quadrant.
Alors, ![]()
![]()
![]()
Angle de base![]()
Avec le ![]() qui est
qui est ![]() ,quatrième quadrant
,quatrième quadrant
Alors, ![]()
![]()
![]()
Réponse: ![]()
[/item] [/accordion]
Problème:
Evaluer ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: Evaluer ![]() “]
“]
Solution
![]()
Pour le conjugué nous savons que
![]()
Soit ![]()
Les valeurs de l’angle sont claires.
Nous savons que le module ![]()
![]()
Ce qui signifie:
![]()
![]()
Ce qui donne:
![]()
Calcul normal:
![]()
Module ![]() et angle de base:
et angle de base: ![]() Premier quadrant
Premier quadrant
![]() Cependant
Cependant ![]()
Ce qui signifie:
![]()
Finalement
Réponse: ![]()
[/item] [/accordion]
Exercice 27C ( EARL):
Soit ![]()
Montrer que ![]() et conclure que
et conclure que ![]()
Trouver l’équation quadratique ayant comme racines ![]() et
et ![]() .
.
Et puis montrer que ![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
Notre Solution
Coordonnées polaires:
![]()
![]()
Sachant que:
![]()
Ce qui donne:
![]()
Les 5 racines, ceci avec les deux membres nulls ![]()
Ce qui donne
![]()
Evaluons chaque facteur pour obtenir les 5 racines:
Avec ![]()
![]()
![]()
![]()
![]()
Les racines sont:
![]() and
and ![]()
Le produit:
![]()
![]()
On peut changer ce qui suit:
![]() qui devient
qui devient
![]()
![]()
En covertissant:
![]()
![]()
Soit ![]()
![]()
![]()
![]()
On sait que ![]() comme l’angle est au premier quadrant.
comme l’angle est au premier quadrant.
![]()
Finalement:
Réponse: ![]()
[/item] [/accordion]
Exercice 28C (EARL)
Trouver le module et l’argument des complexes suivants:
![]() et
et ![]() .
.
Calculer ![]() avec les coordonnées polaires et la forme
avec les coordonnées polaires et la forme ![]() .
.
En déduire ![]() et
et ![]() .
.
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() and
and ![]() “]
“]
Notre Solution:
![]()
module:
![]()
![]()
![]()
![]()
![]()
module:
![]()
![]()
![]()
![]()
maintenant calculer ![]()
![]()
![]()
En forme polaire:
![]()
![]()
![]()
On peut dire:
![]()
![]()
![]()
![]()
![]()
Finalement
Réponse: ![]() and
and ![]()
[/item] [/accordion]
Exercice 30 B (EARL):
En se servant des racines 7ièmes de -1, montrer que:
![]()
utiliser une méthode similaire pour trouver:
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour trouver la solution de: ![]() “]
“]
Solution:
![]()
Module:![]()
Argument:![]() and
and ![]()
Ce qui donne ![]()
![]()
Les racines 7ièmes:
![]() with
with ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La somme des racines est ![]()
![]()
Ce qui donne:
![]()
De la même faςon on peut poser:
![]() et on obtiendra:
et on obtiendra:
![]()
Finalement:
![]()
![]()
[/item] [/accordion]
Résoudre en ![]()
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour trouver la solution de: ![]() “]
“]
Solution:
![]()
![]()
![]()
Finalement:
Réponse : ![]()
[/item] [/accordion]
Résoudre ![]()
Plotter les racines et calculer l’aire de la figure ainsi formée.
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour trouver la solution de: ![]() “]
“]
Solution:
Module:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalement:
Réponses: ![]()
[/item] [/accordion]
Mettre sous la forme ![]() :
:
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
Solution:
![]()
A noter que ![]() est de 1 radian ou
est de 1 radian ou ![]() en degrés.
en degrés.
Alors:
![]()
Finalement:
Réponse: ![]()
[/item] [/accordion]


Be the first to comment