Order of Operations

Whether you are programming or dealing with simple Algebra factors, it is essential to know the order of operations.
It is obvious that even when we look at some social media small games, we can see that many do not remember the order of operations.
If I ask the result of $5+3 \times8^2$ , half of the answers will go wrong.

The following rules must be followed:
1. Complete all the operations within the parentheses before the outside operations.
2. Evaluate all exponential expressions
3. Do all multiplications and divisions in order from left to right.
4. Finish with all additions and subtractions in order from left to right.
This is what most describe as PEMDAS (memorize as Please Excuse My Dear Aunt Sally).
Task 1: $5+3 \times8^2$
There is no parentheses.
There is an exponent $8^2=64$
Now we have $5+3\times 64$
From left to right we hit $3 \times 64=192$
Now we are left with $5+192$
From left to right we hit one addition $5+192=197$ which is the answer.

Exercise:
1. Simplify and Calculate:
$\mathbf{3+[10(9-2^{2})]}$

(1) $\begin{equation*} \begin{split} 3+[10(9-2^{2})]&=3+[10(9-4)]\\ &=3+[10(5)]\\ &=3+(50)\\ &=3+50\\ &=53 \end{split} \end{equation*}$

2. Simplify and Calculate:
$\mathbf{20-2\cdot\;6+12^{2}+(9-2)\cdot\;3}$

(2) $\begin{equation*} \begin{split} 20-2\cdot\;6+12^{2}+(9-2)\cdot\;3&=20-2\cdot\;6+12^{2}+(7)\cdot\;3\\ &=20-2\cdot\;6+144+7\cdot\;3\\ &=20-12+144+21\\ &=8+144+21\\ &=152+21\\ &=173 \end{split} \end{equation*}$

Post Views: 330

Order of Operations

Order of Operations

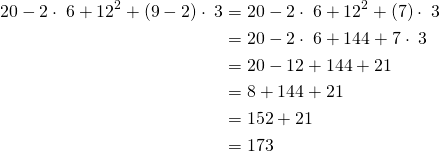
Be the first to comment

Leave a Reply Cancel reply