Ostrogradsky’s method

July 23, 2023 Mouctar Calculus 0

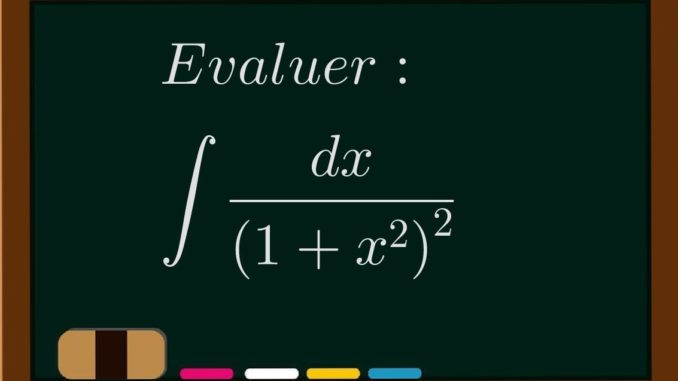
This method is used to isolate the algebraic part in indefinite integral of the rational functions
{\displaystyle \int \frac{P(x)}{Q(x)}\mathrm{d} x=\frac{P_1(x)}{Q_1(x)}+\int \frac{P_2(x)}{Q_2(x)}}

To find Q_1(x):
This is the Greatest Common divisor of Q(x) and its derivative.

To find Q_2(x):
Q_2(x)=\frac{Q(x)}{Q_1(x)}

To find P_1(x) and P2_(x) we use partial fractions decomposition.

Finally we take the derivative of both sides.
We carry out the integration.

Evaluate: {\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}}

P(x)=1
{\displaystyle Q(x)=(1+x^2)^2}
{\displaystyle Q'(x)=4x(1+x^2)}

Greatest common divisor of Q(x) and Q'(x)
{\displaystyle Q_1(x)=(1+x^2)}

{\displaystyle Q_2(x)=\frac{Q(x)}{Q_1(x)}=\frac{(1+x^2)^2}{1+x^2}=1+x^2}
Now we put all together:

{\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}=\frac{Ax+B}{1+x^2}+\int \frac{Cx+D}{1+x^2}}

Now we take the derivative of both sides:
\left({\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}=\frac{Ax+B}{1+x^2}+\int \frac{Cx+D}{1+x^2} }\right)'

We get:
{\displaystyle \frac{\mathrm{d} x}{(1+x^2)^2}=\left(\frac{Ax+B}{1+x^2}\right)'+ \frac{Cx+D}{1+x^2}}
{\displaystyle \left(\frac{Ax+B}{1+x^2}\right)'=\frac{A(1+x^2)-2x(Ax+B)}{(1+x^2)^2}}

{\displaystyle \left(\frac{Ax+B}{1+x^2}\right)'=\frac{A-2Bx-Ax^2}{(1+x^2)^2}}

{\displaystyle \frac{\mathrm{d} x}{(1+x^2)^2}= \frac{A-2Bx-Ax^2}{(1+x^2)^2}+\frac{Cx+D}{1+x^2}}

Common denominator:
{\displaystyle 1=(A-2Bx-Ax^2)+(Cx+D)(1+x^2)}

{\displaystyle 1=A-2Bx-Ax^2+Cx+D+Cx^3+Dx^2}

{\displaystyle 1=(A+D)+(C-2B)x+(-A+D)x^2+Cx^3}

Checking the equality:
{\displaystyle A+D=1 \Rightarrow D=1-A}

{\displaystyle C-2B=0 \Rightarrow C=2B}

{\displaystyle C=0 }

{\displaystyle D-A=0 \Rightarrow A=D }

But:
{\displaystyle A+D=1 \Rightarrow 2A=1 \Rightarrow A=D=\frac{1}{2}}
{\displaystyle C-2B=0 \Rightarrow C=2B=0}

Putting it back:

{\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}= \frac{x}{2(1+x^2)}+\frac{1}{2}\int \frac{\mathrm{d} x}{1+x^2}}

Finally:
{\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}= \frac{x}{2(1+x^2)}+\frac{1}{2}\tan^{-1}x+C}

Alternate methods:
Trigonometric substitution:
Evaluate: {\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}}

Let:

{\displaystyle x=\tan \theta}
{\displaystyle \mathrm{d} x=\sec^2 \theta \mathrm{d} \theta}
{\displaystyle 1+x^2=1+\tan^2 \theta=sec^2 \theta}
{\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}=\int \frac{sec^2 \theta }{(\sec^2)^2 \theta}\mathrm{d} \theta}
{\displaystyle \int \frac{sec^2 \theta }{(\sec^2)^2 \theta}\mathrm{d} \theta=\int \frac{\mathrm{d} \theta}{sec^2 \theta}=\int \cos^2 \theta \mathrm{d} \theta}

{\displaystyle \cos 2\theta=\cos^2 \theta- \sin^2 \theta=2\cos^2 \theta-1 \Rightarrow \cos^2 \theta= 1+ \cos 2\theta }

{\displaystyle \int \cos^2 \theta \mathrm{d} \theta=\frac{1}{2}\int (1+\cos 2\theta)\mathrm{d} \theta}

{\displaystyle \int \cos^2 \theta \mathrm{d} \theta=\frac{1}{2}\int \mathrm{d} \theta+ \frac{1}{2}\int \cos (2\theta)\mathrm{d} \theta}

{\displaystyle \int \cos^2 \theta \mathrm{d} \theta=\frac{\theta}{2}+\frac{\sin 2\theta}{4}+C }

Back to x:
{\displaystyle x=\tan \theta \Rightarrow \theta=\tan^{-1}x}
{\displaystyle \sin 2\theta=\frac{2x}{1+x^2}}

Finally:
{\displaystyle \int \frac{\mathrm{d} x}{(1+x^2)^2}=\frac{x}{2(1+x^2)}+\frac{1}{2}\tan^{-1}x+C}



Print Friendly, PDF & Email
Post Views: 1,121

Be the first to comment

Leave a Reply

Your email address will not be published.


*