VOLUME OF A RECTANGULAR SOLID:
The volume of a rectangular solid is the product of the Base B and the height h.
-Volume of a prism:
The volume of a prism is the product of the Area B of a base and the height h.
AREAS AND VOLUMES OF A CYLINDER:
A cylinder is a figure formed by two congruent circular regions contained in parallel planes along with all segments having an endpoint on each circle and parallel to the line joining the centers of the circles.
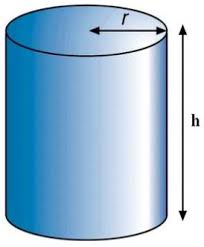
Lateral Area of a Right Cylinder:
The Lateral area L.A. of a right Cylinder is the product of the circumference C of a base and the height h.
-The Total Area:
-Volume of the Cylinder:
-AREAS AND VOLUME OF A PYRAMID:
A pyramid is a polyhedron formed by a polygonal region in a plane 
a point 
not in plane and the triagular regions formed by joining the vertices of the polygonal region with .
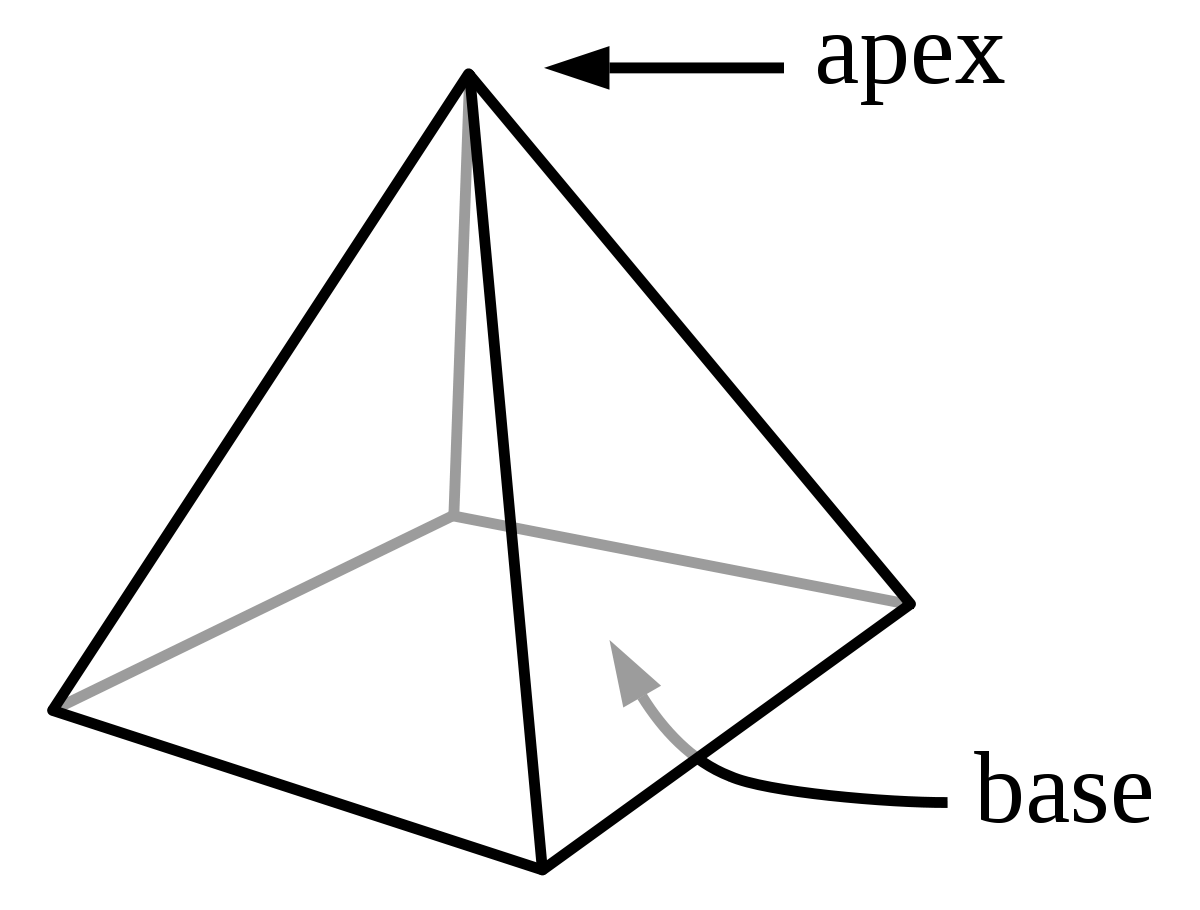
-The lateral faces of a regular pyramid are congruent isosceles triangles.
-The Lateral Area L.A. of a regular pyramid is one half the product of the slant height 
and the perimeter 
of the base.
The total area T.A. of a pyramid is the sum of the lateral area and the area of the base:
-The volume V of a pyramid is one third the product of the area B of the base and the height h.
AREAS AND VOLUME OF A CONE:
A cone is a figure formed by a circular region, a point M not in the plane of the circle, and all the segments joining a point of the circle to M.
Lateral Area of a Right Cone:
The Lateral Area L.A. of a right cone is one half the product of the circumference C of its base and its slant height
Volume of a cone:
The volume V of a Cone is one third the product of the area of the base 
and its height 
.
AREA AND VOLUME OF A SPHERE:
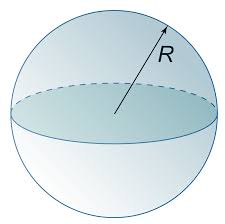
The volume of a sphere of radius
is given by:
-Area of a sphere:
The area of a sphere of Radius R is:
Be the first to comment