Polynomial Functions
We have already discussed a particualar polynomial, the quadratic.In this journey, we are going to extend our knowledge to other types of polynomials.
The purpose here is to know how to manipulate the polynomials in our daily tasks.
In this site we will have more practice than theory.We have already seen that a monomial can be a number, a variable or a product of both.
A polynomial, on the other hand, is a monomial or a combination of monomials.An example is:
![]()
In this function ![]() , is the leading coefficient and
, is the leading coefficient and ![]() is aclled the
is aclled the ![]() .We also note that
.We also note that ![]() is the constant.
is the constant.
The exponents are whole numbers while the coefficients are real numbers.
Polynomial:
![]()
Exponents are whole numbers and coefficients are real numbers.
Not a polynomial:
![]()
Some exponents are not whole numbers.
Operations on Polynomials:
Direct substitution:
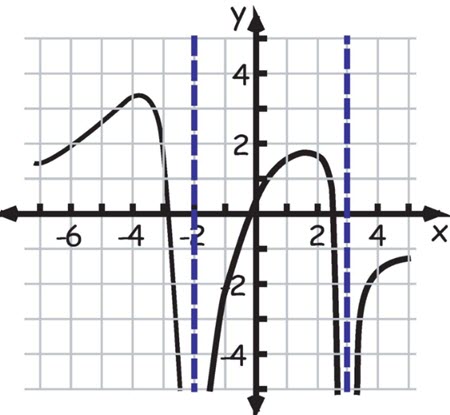
Example:Evaluate: ![]() when
when ![]()
We get:![]()
(1) 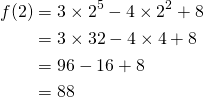
Adding or Subtracting Polynomials:
To add or subtract polynomials, we just add or subtract the coefficients of like terms.
Add: ![]() and
and ![]()
We add like terms:
![]()
Multiplying polynomials
To multiply polynomials, we multiply each term of the first polynomial by each term of the other polynomial.
This reminds us of the identities seen in another course in this site.
(2) 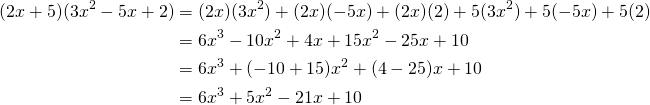
Factoring a polynomial:
A polynomial is factored completely if it is written as a product of unfactorable polynomials with integer coefficients.
Example:
Factor ![]()
(3) 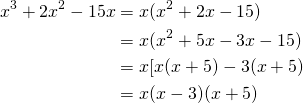
We just used factoring by grouping.
Another example:
Factor:![]()
(4) 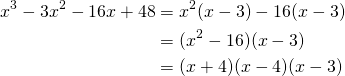
Power function:
The power function has the form:![]()
In this function, the coefficient is a real number ![]() , and
, and ![]() is an integer.
is an integer.
The power function has some properties worth noting.
If ![]() and
and ![]() is even we have:-The function is said to be
is even we have:-The function is said to be ![]() . This means the graph is symmetric with respect to the y-axis.-The domain is the set of all real numbers with a range being the set of nonnegative numbers.
. This means the graph is symmetric with respect to the y-axis.-The domain is the set of all real numbers with a range being the set of nonnegative numbers.
-This graph contains the main points ![]() ,
,![]() and
and ![]()
If ![]() and
and ![]() is odd we have:-The function is said to be
is odd we have:-The function is said to be ![]() .
.
This means the graph is symmetric with respect to the origin.-The domain and range are all the set of all real numbers.
-This graph contains the main points ![]() ,
,![]() and
and ![]()
We will cover later the variation of functions.
Solving polynomials, finding zeros
REAL ZEROS:
A polynomial of degree ![]() cannot have more a number of real zeros more than
cannot have more a number of real zeros more than ![]()
Example:![]()
cannot have more than 4 real zeros.
Rational zeros theorem:
For:
![]() if
if ![]() and
and ![]()
with all integer coefficients, when ![]() is a rational zero of
is a rational zero of ![]() then
then ![]() is a factor of
is a factor of ![]() and
and ![]() is a factor of
is a factor of ![]() .
.
Example:
![]()
We have ![]() the
the ![]() factors are
factors are ![]() ,
, ![]() ,
,![]() ,
,![]()
![]() the
the ![]() factors are
factors are ![]() ,
, ![]()
We check all the possible ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
THEOREM: A polynomial function of odd degree that has real coefficients has at least one real zero.
THEOREM: For a polynomial function ![]() . If
. If ![]() and if
and if ![]() and
and ![]() are of opposite sign, then there is at least one real zero of
are of opposite sign, then there is at least one real zero of ![]() between
between ![]() and
and ![]() .
.
Complex Zeros of a polynomial:A complex polynomial function ![]() of degree
of degree ![]() has at least one complex coefficient.
has at least one complex coefficient.
A polynomial function ![]() of odd degree with real coefficients has at least one real zero.
of odd degree with real coefficients has at least one real zero.
Third degree or cubic function solutions: Girolamo Cardano formula
We are going to study the third degree equation and find an easy way to find the solutions.
The Cubic formula we are going to use will have variations, according to the situation.
Trigonometric Solutions:
Given:
![]()
Let’s depress the equation.
![]()
We apply the substitution
![]()
![]()
We get the deprecated function.
![]()
Please note that when ![]() , we can simply deduct the 3 values of
, we can simply deduct the 3 values of ![]() from those of
from those of ![]() .
.
First case: when ![]() and
and ![]()
We proceed as follows:
![]()
When we replace ![]() in our equation:
in our equation:
![]()
![]()
![]()
![]()
By simple division we get:
![]()
Let’s simplify the left side:
(5) 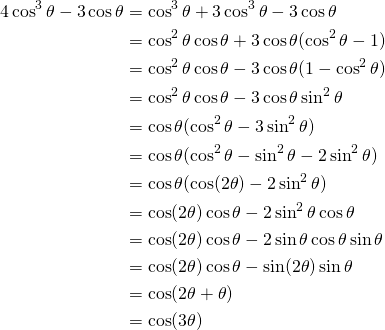
The simplified Equation is:
![]()
We can now find ![]() ,
, ![]() and
and ![]() .
.
Second case: when ![]() and
and ![]()
Here we say:
![]()
The same transformations yield:
![]()
And:
![]()
Third case: when ![]()
Here we say:
![]()
The same transformations yield:
![]()
And:
![]()
Trigonometric method for complex conjugates:
From
![]()
With:
![]()
First case: when ![]()
Let’s calculate ![]() and
and ![]()
![]()
Now:
![]()
The ![]() values:
values:
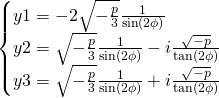
For ![]() values we just apply
values we just apply ![]()
Second case: when ![]()
Let’s calculate ![]() and
and ![]()
![]()
Now:
![]()
The ![]() values:
values:
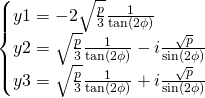
For ![]() values we just apply
values we just apply ![]()
Other methods:
In this case we consider the same steps but with more details
![]()
The same steps above will be used
We get:
![]()
This is of the form:
![]()
So we have to calculata ![]() and
and ![]()
![]()
and
![]()
Next we calculate ![]() and
and ![]()
![]()
![]()
We can now deduct the 3 roots:
![]()
![]()
![]()
Let D be:
![]()
If ![]() , the equation has one real root and 2 complex roots
, the equation has one real root and 2 complex roots
If ![]() , the equation has one root
, the equation has one root ![]() and a double root
and a double root ![]()
If ![]() , the equation has three real roots
, the equation has three real roots
Worked examples:
1.Find the solutions of the equation:![]()
Solution

Factoring by ![]()
We get:![]()
Now let’s factor the quantity:![]()
(6) 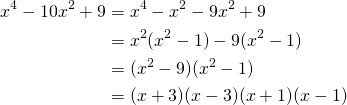
Now put together:![]()
Means:![]()
![]()
Each of the factors can verify the relationships.
![]()
![]()
![]()
![]()
![]()
We have now the five solutions:
Answer: ![]()
Signs of zeros of a polynomial
Descartes’ Rule of signs theorem
If ![]() is a standard polynomial function:
is a standard polynomial function:
-The number of positive real zeros of ![]() is either equals the number of variations in the sign of the non-zero coefficients of
is either equals the number of variations in the sign of the non-zero coefficients of ![]() or else that number less than an even integer.
or else that number less than an even integer.
-The number of negative real zeros of ![]() is either equals the number of variations in the sign of the non-zero coefficients of
is either equals the number of variations in the sign of the non-zero coefficients of ![]() or else that number less than an even integer.
or else that number less than an even integer.
Example:
![]()
-At least 5, 3 or 1 positive zeros.(5 changes in the sign)
![]()
-No sign variation means no negative root.


Be the first to comment