
Fonctions polynomiales
Nous avions déjà parlé d’un polynôme particulier, la fonction quadratique. Dans les prochains chapitres, nous allons enrichir notre connissance en abordant d’autres types de polynômes. Le seul objectif étant de nous permettre de pouvoir manipuler ces fonctions dans nos taches quotidiennes.
Ce site s’occupe plus de la pratique que de la théorie. Nous savons que le monôme peut être un nombre, une variable ou une combinaison des deux.
Un polynôme est un monôme ou une combinaison de monômes.
![]()
Dans cette function, ![]() , est le coefficient dominant,
, est le coefficient dominant, ![]() est le
est le ![]() .Nous constatons aussi que
.Nous constatons aussi que ![]() est une constante.
est une constante.
Les exposants sont des nombres entiers tandis que les coefficients sont des nombre réels
Polynôme:
![]()
Pas un polynôme car certains exposants ne sont pas entiers:
![]()
Operations sur les polynômes:
Substitution:
Exemple:Evaluer: ![]() pour
pour ![]()
Nous vons:![]()
(1) 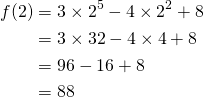
Addition et soustraction de polynômes
Pour faire l’addition ou la soustraction de polynômes,on fait l’addition ou la soustraction des termes semblables.
Add: ![]() and
and ![]()
Addition des termes semblables:
![]()
Multiplication des polynômes
Pour multiplier deux polynômes, on multiplie chauqe terme du premier par chaque terme du second.
Nous avons effectuer ce genre de multiplication dans les calculs des identités remarquables.
(2) 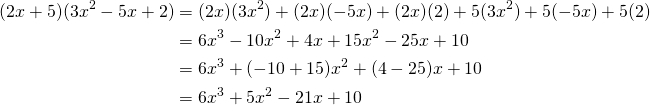
Mise en facteurs d’un polynôme
Une factorisation d’un polynôme consiste à l’écrire sous la forme de facteurs irreductibles
Exemple:
Factoriser ![]()
(3) 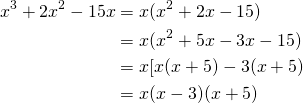
Ici en regroupant.
Un autre exemple:
Factoriser: ![]()
(4) 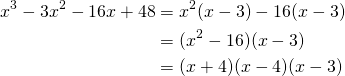
Fonction puissance:
Une fonction de la forme: ![]()
Avec cette fonction,le coefficient est un nombre réel ![]() , et
, et ![]() est un entier.
est un entier.
Quelques propriétés importantes:
Si ![]() et
et ![]() est pair nous avons:-Une fonction
est pair nous avons:-Une fonction ![]() . Symetrie par rapport à l’axe des y.-Le domaine est est l’ensemble des nombres nonnegatifs.
. Symetrie par rapport à l’axe des y.-Le domaine est est l’ensemble des nombres nonnegatifs.
-Le graphique contient ces quelques points ![]() ,
,![]() and
and ![]()
Si ![]() et
et ![]() est impair:-La fonction est dite
est impair:-La fonction est dite ![]() .
.
Ici il y a symétrie pa rapport à l’origine.-Le domaine est ici aussi l’ensmble de tous les réels.
-Le graphique contient ces quelques points ![]() ,
,![]() and
and ![]()
Trouver les zeros d’un polynôme
ZEROS REELS:
un polynôme de degré ![]() ne peut avoir un nombre de racines supérieur à
ne peut avoir un nombre de racines supérieur à ![]()
Exemple:![]()
ne peut avoir un nombre de racines supérieur à 4.
Théorême des zeros rationnels:
Pour:
![]() , si
, si ![]() and
and ![]()
por tous les coefficients, lorsque ![]() est un zero de
est un zero de ![]() alors
alors ![]() est un facteur de
est un facteur de ![]() et
et ![]() un facteur de
un facteur de ![]() .
.
Exemple:
![]()
Nous avons ![]() les
les ![]() facteurs sont
facteurs sont ![]() ,
, ![]() ,
,![]() ,
,![]()
![]() the
the ![]() factors are
factors are ![]() ,
, ![]()
Nous essayons toutes les combinaisons ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
THEOREME: Une fonction polynomiale de degré impair ayant des coefficients réels a au moins un zero réel.
THEOREME: Pour une fonction polynomiale ![]() . si
. si ![]() et si
et si ![]() et
et ![]() sont de signes contraires, alors il existe au moins un zero de
sont de signes contraires, alors il existe au moins un zero de ![]() entre
entre ![]() et
et ![]() .
.
Racines complexes:une fonction polynomiale complexe ![]() de degré
de degré ![]() a au moins un zero complexe.
a au moins un zero complexe.
Une fonction polynomiale ![]() de degré impair ayant des coefficients réels a au moins un zero réel.
de degré impair ayant des coefficients réels a au moins un zero réel.
TSolutions de la fonction cubique: Formule de Girolamo Cardano
Les considerations qui suivent vont nous aider à trouver les solutions de l’équation de troisième degré.
Nous examinerons des cas variés.
Solutions Trigonometriques:
On donne:
![]()
Reduisons l’équation
![]()
On procède à la substitution:
![]()
![]()
On obtient:
![]()
A noter que quand ![]() , on fait une simple deduction des 3 valeurs de
, on fait une simple deduction des 3 valeurs de ![]() à partir de
à partir de ![]() .
.
Premier cas: Quand ![]() et
et ![]()
On obtient:
![]()
En remplaçant ![]() dans l’équation:
dans l’équation:
![]()
![]()
![]()
![]()
Une petite division donne:
![]()
Simplifions le premier membre:
(5) 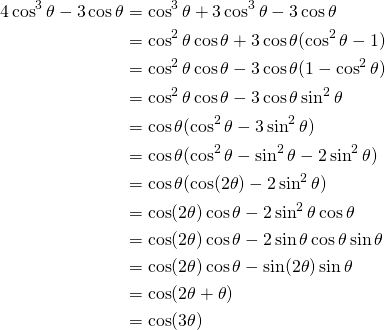
Nous obtenons:
![]()
On porra alors trouver ![]() ,
, ![]() and
and ![]() .
.
Second cas: Lorsque ![]() et
et ![]()
Nous posons:
![]()
La transformation donne:
![]()
et:
![]()
Troisième cas: Lorsque ![]()
Nous obtenons
![]()
La transformation donne:
![]()
Et:
![]()
Méthode trigonométrique pour les complexes conjugués:
De la forme
![]()
Avec
![]()
Prmier cas: Avec ![]()
On Calcule ![]() and
and ![]()
![]()
Alors
![]()
les valeurs de ![]() :
:
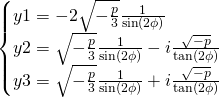
Pour les valeurs de ![]() on effectue
on effectue ![]()
Second cas:Avec ![]()
On cherche ![]() and
and ![]()
![]()
Alors:
![]()
Les valeurs de ![]() :
:
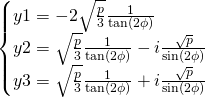
Pour ![]() On effectue
On effectue ![]()
Autres Chemins:
On utilise un cheminement similaire mais avec plus de détails:
![]()
On procède de la même façon.
Nous avons
![]()
La forme
![]()
On cherche ![]() et
et ![]()
![]()
Et puis
![]()
Ensuite nous cherchons ![]() et
et ![]()
![]()
![]()
On en déduit les 3 racines:
![]()
![]()
![]()
Avec D comme:
![]()
Si ![]() , Nous avons une racine réelle et 2 racines complexes.
, Nous avons une racine réelle et 2 racines complexes.
Si ![]() , nous avons une racine
, nous avons une racine ![]() et une racine double
et une racine double ![]()
Si ![]() , 3 racines réelles.
, 3 racines réelles.
Exemples:
1.Trouver les solutions de :![]()
Solution

Factorisant par ![]()
On a:![]()
Factorisons:![]()
(6) 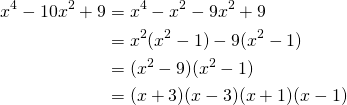
En assemblant: ![]()
Cela veut dire que :![]()
![]()
Chaque facteur vérifie l’égalité.
![]()
![]()
![]()
![]()
![]()
Les 5 solutions
Réponse: ![]()
[/item] [/accordion]
Signes des zeros d’un polynôme
Règle de Descartes
Si ![]() est une fonction polynomiale:
est une fonction polynomiale:
-Le nombre des zeros positifs réels de ![]() est soit égal au nombre de variations des signes des coefficients non-nuls de
est soit égal au nombre de variations des signes des coefficients non-nuls de ![]() ou alors de ce nombre diminué d’un entier pair.
ou alors de ce nombre diminué d’un entier pair.
-Le nombre des zeros négatifs réels de ![]() est soit égal au nombre de variations des signes des coefficients non-nuls de
est soit égal au nombre de variations des signes des coefficients non-nuls de ![]() ou alors de ce nombre diminué d’un entier pair.
ou alors de ce nombre diminué d’un entier pair.
Exemple:
![]()
-Au moins 5, 3 ou 1zeros positifs.(5 changements de signes)
![]()
-Pas de variation de signes de ![]() . Pas de racine négative.
. Pas de racine négative.


Be the first to comment