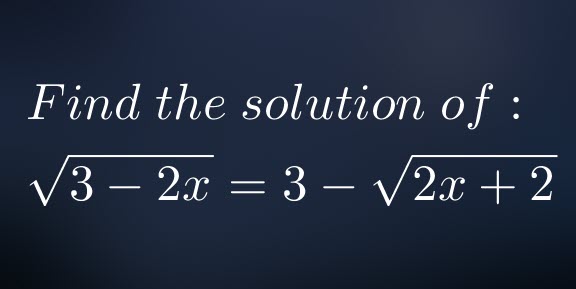
Radical Expressions and Exponential Notations

Exponential notations help us express long expressions into shorthand notations.
For example if we have $5\cdot5\cdot5\cdot5\cdot5\cdot5$ we can see that we are multiplying 5 by itself 6 times. This is easy for short expressions.
However, when we have longer expressions, it becomes very hard to write them in a paper.

In our example, let’s call the number being multiplied (5) the “base”.
The number of times we are multiplying (6) is called the “exponent”.
We can write it as $5^6$ .
If we have a base $x$ multiplied $n$ times where $n$ is an integer greater than 1, we can write it as $x^n$ . We read : $x$ to the $nth$ power or simply $x$ to the $nth$ .
If $n=2$ , it is read “ $x$ squared” and if $n=3$ , it is read “ $x$ cubed”.
The major problem students encounter is thinking that $x^n$ equal $x\cdot n$ . Please note that $7^2=7 \cdot 7= 49$ and not $7 \cdot 2=14$ .

Rules:

$x^1=x$
$x^{-n}=\frac{1}{x^n}$
We get $x^0=x^{1-1}=x^1 \cdot x^{-1}=x^1 \cdot \frac{1}{x^1}=\frac{x}{x}=1$ with $x$ non-zero.

Product:

-To raise a product to a power, raise all parts to that power: $(3xy)^5=3^5 \cdot x^5 \cdot y^5$
While we are in the multiplication, note that $x^m \cdot x^n= x^{(m+n)}$
Example: $(3x)^2 \cdot (3x)^5=(3x)^{(2+5)}=(3x)^7=3^7 \cdot x^7$

Quotient:

$\frac{x^m}{x^n}=x^{(m-n)}$
$\frac{x^5}{x^4}=x^{(5-4)}=x^1=x$

Another interesting rule:
$(\frac{x}{y})^n=\frac{x^n}{y^n}$
$(\frac{x}{y})^4=\frac{x^4}{y^4}$

$(\frac{x}{y})^{-n}= (\frac{y}{x})^n$
$(\frac{x}{y})^{-8}= (\frac{y}{x})^8$

Power:

$(x^m)^n=x^{mn}$
$(x^2)^5=x^{2 \cdot 5}=x^{10}$

Roots or radicals

Roots or radicals can be used to solve problems. In calculus or other complex calculations, it will be easier to convert them to exponents and then revert back to radicals after all calculations.
Remember: $\sqrt[n]{x^m}=x^{\frac{m}{n}}$

Square roots:

A number $x$ is square root of $y$ if we have $x^2=y$ .
Every real number greater than zero has two square roots. Negative numbers do not have real numbers as square roots.
The square root of $0$ is $0$ .
The square root of a positive number $x$ is the positive root noted $\sqrt{x}$
$\sqrt{81}=9$
$-\sqrt{100}=-10$
$\sqrt{\frac{25}{64}}=\frac{5}{8}$ . We can always use rules learned with the Exponential notations.
The symbol $\sqrt{}$ is called the “radical”.
The expression under the radical is the “radicand”
Together they form the “radical expression”
As a rule: $\sqrt{x^2}=\left |{x}\right |$ .

Cubic roots

The number $x$ is the cube root of $y$ if its third power is $y$ .
Every real number has a single cube root.
$\sqrt[3]{125}=5$
$\sqrt[3]{-\frac{8}{125}}=-\frac{2}{5}$

General Rule:

If $k$ is an odd natural number, then for any real number $x$ , we have $\sqrt[k]{x^k}=x$
If $k$ is an even natural number, we use the absolute value unless $x$ is greater or equal to $0$ :
$\sqrt[k]{x^k}=\left |{x}\right |$ .

Product rules for radicals:

They are similar to those for the Exponentials.
For any real numbers $x$ and $y$ and any index $k$ with $k \geq 2$
$\sqrt[k]{xy}=\sqrt[k]{x}\cdot \sqrt[k]{y}$
$\sqrt{12}=\sqrt{4 \cdot 3}=\sqrt{4}\cdot \sqrt{3}=2 \sqrt{3}$ .

Rationalization

When dealing with radicals, it is often asked to rationalize the denominator which is irrational. Various methods exist depending on what we have in the denominator.
Example :
$\frac{x}{\sqrt{5}}=\frac{x \cdot \sqrt{5}}{\sqrt{5}\cdot \sqrt{5}}=\frac{x \sqrt{5}}{5}$