

Représentation graphique des fonctions trigonométriques
Pour voir ces fonctions trigonométriques de façon claire, nous allons les représenter sur les mêmes graphiques que leurs reciproques.
Cele signifie que la courbe ![]() et la courbe
et la courbe ![]() seront ensemble.
seront ensemble.
Cela signifie aussi que la courbe ![]() et la courbe
et la courbe ![]() auront le même graphe
auront le même graphe
Et finalement lea courbe ![]() et la courbe
et la courbe ![]() uront le même graphe.
uront le même graphe.
Courbes de:

Intersection aux maximum et minimums de leur valeurs
La fonction ![]() n’est pas définie lorsque
n’est pas définie lorsque ![]() . Ce sont les asymptôtes verticales de la fonction
. Ce sont les asymptôtes verticales de la fonction ![]()
Courbes de:

Nous remarquons aussi que ces deux fonctions ont leur intersection aux minimums et maximums de leurs valeurs.
La fonction ![]() n’est pas définie quand
n’est pas définie quand ![]() . Ce sont les asymptôtes verticales de la fonction
. Ce sont les asymptôtes verticales de la fonction ![]()
Courbes de:
L’intersection a lieu aux points quand ![]() .
.
Ces points correspondent aux multiples d’un seul angle ![]() . Chacune de ces fonctions a son asymptôte quand l’autre fonction est
. Chacune de ces fonctions a son asymptôte quand l’autre fonction est ![]() .
.

Ces courbes montrent que ces fonctions reprennent les valeurs identiques après un certain cycle correspondant à certaines valeurs de ![]() . Ces fonctions sont dites periodiques.
. Ces fonctions sont dites periodiques.
La reprise de forme s’appelle ![]() .
.
Sommaire de l’allure de ces fonctions:
La fonction “sinus”:
Avec A,B,C et D constants, nous voyons que la représentation devient facile si nous nous servons de la fonction de base ![]() et nous utilisons des techniques connues.
et nous utilisons des techniques connues.
L’Amplitude:
L’amplitude ![]() est la mesure du maximum ou du minimum à partir de la base
est la mesure du maximum ou du minimum à partir de la base ![]() .
.
L’amplitude est toujours positive. ![]() . La courbe de
. La courbe de ![]() est multipliée par
est multipliée par ![]() .
.
Période:
C’est la largeur horizontale d’un cycle ou une onde. Après une onde, l’allure est reprise.
Nous voyons que la fonction ![]() ,
, ![]() ,
, ![]() and
and ![]() se repète après
se repète après ![]() .
.
Pour la fonction:
![]() , nous connaissons que la periode de la fonction de base
, nous connaissons que la periode de la fonction de base ![]() est
est ![]()
La periode sera alors de:
Fréquence:
La fréquence de la fonction est l’inverse de sa période.
Le déphasage:
Décallage horizontal de la fonction de base qui se calcule comme suit:
Déplacement vertical:
C’est simplement ![]()
Toutes ces valeurs seront appliquées comme si on avait à faire à une fonction ordinaire:
La periode est un outil majeur dans la résolution des équations trigonométriques.
Pour les fonctions tangente et cotangentes on utilisera les mêmes principes, connaissant que la periode de la fonction de base est de ![]() .
.
Le déphasage est important pour la tangente:
![]() . Le premier cycle commence à ‘zero’ qui est “dephasage vers la droite de l’origine”. Les asymptôtes seront à
. Le premier cycle commence à ‘zero’ qui est “dephasage vers la droite de l’origine”. Les asymptôtes seront à ![]() vers la gauchedu cycle de départ, et une autre sera à
vers la gauchedu cycle de départ, et une autre sera à ![]() vers la droite du cycle de départ.
vers la droite du cycle de départ.
Pour faire le graphe de 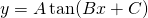 :
:
Pour des réels non-nuls ![]() et
et ![]()
-La periode est ![]() et le déphasage est
et le déphasage est ![]()
On trouve deux asymptôtes consécutives en traitant:
![]()
Pour la cotangente on utilse des techniques similaires.
Exemple1:
Trouver amplitude et periode de ![]()
Ici:
![]() and
and ![]()
La periode est de ![]()
Exemple2:
![]()
Amplitude: ![]()
Periode: ![]()
Exemple 3:
![]()
![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
L’amplitude: ![]()
La periode: ![]()
Le dephasage: ![]()
The premier intervalle est ![]() pour une periode de
pour une periode de ![]() .
.
On peut aussi utiliser la méthode suivante:
L’intervalle qui contient un cycle se trouve en traitant l’inégalité suivante:
![]()
Nous avons:
![]()
![]()
Exemple 4:
Trouver l’amplitude, la periode et le déphasage de l’équation:
![]()
Amplitude:
![]()
Periode: ![]()
Déphasage
![]()
On graphe entre:
![]()
![]()


Be the first to comment