Selected Trigonometry Exercises
These are the selected trigonometry exercises and problems to solidify the concepts shown in this site.
Exercise 1:
A surveyor observes that at a point ![]() , located on level ground a distance 25.0 feet from the base
, located on level ground a distance 25.0 feet from the base ![]() of a flagpole, the angle between the ground and the top of the pole is
of a flagpole, the angle between the ground and the top of the pole is ![]() . What is the height of the pole to the nearest hundredth of the feet.
. What is the height of the pole to the nearest hundredth of the feet.
Solution:
From the graph we don’t know the hypothenuse and we don’t need to calculate it.
We can use the tangent in this situation:
![]()
This yields:
![]()
![]()
![]()
Exercise 2:
Show that the following identity is true:
![]()
Solution:
From the left we can write:
(1) 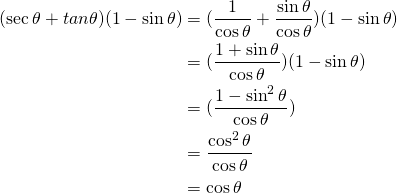
Finally we can say that:
![]()
Exercise 3:
The peak of Mt. Fuji in Japan is approximately12,400 feet high.
A student, several miles away, finds that the angle between the level ground and the peak is ![]() . How far is the student from the point on the level ground directly beneath the peak?
. How far is the student from the point on the level ground directly beneath the peak?
Solution:
![]()
This gives:
![]()
![]()
![]()
Exercise 4:
Stonehenge in Salisbury Plains, England, was constructed using solid stone blocks weighing over 99,000 pounds each. Lifting a single stone alone required 550 people, who pulled the stone up a ramp inclined at an angle of ![]() . What is the approximate distance a stone was moved in order to raise it to a height of 30 feet?
. What is the approximate distance a stone was moved in order to raise it to a height of 30 feet?
Solution:
Here we can see that:
![]()
This gives:
![]()
![]()
![]()
Exercise 5:
From the top of a building that overlooks an ocean, an observer watches a boat sailing directly toward the building. If the observer is 100 feet above sea level and if the angle of depression of the boat changes from ![]() to
to ![]() during the period of the observation, approximate the distance travelled by the boat.
during the period of the observation, approximate the distance travelled by the boat.
Solution:
![]()
This gives:![]()
![]()
This yields:
![]()
The distance:![]()
![]()
![]()
Exercise 6:
The highest advertising sign in the world is a large letter ![]() situated at the top of a 73-story First Interstate World Center building in Los Angeles. At a distance of 200 feet from a point directly below the sign, the angle between the ground and the to top of the sign is
situated at the top of a 73-story First Interstate World Center building in Los Angeles. At a distance of 200 feet from a point directly below the sign, the angle between the ground and the to top of the sign is ![]() . What is the heght of the top of the sign?
. What is the heght of the top of the sign?
Solution:
![]()
![]()
![]()
Exercise 7:
Simplify: ![]()
Solution:
We have:
(2) 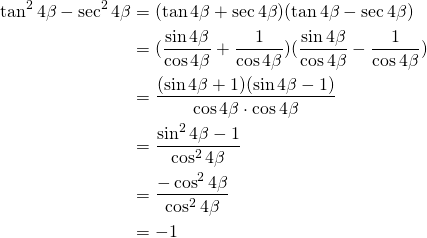
Finally:![]()
Exercise 8:
Simplify: ![]()
Solution:
We have:
(3) 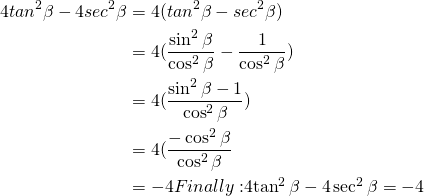
Exercise 9:
Two stars that are close may appear to be one. The ability of a telescope to separate their images is called its resolution. A smaller resolution means a better ability for the telescope to separate images in the sky. In a refracting telescope, resolution ![]() can be improved by using a lens with a larger diameter
can be improved by using a lens with a larger diameter ![]() . The relationship between
. The relationship between ![]() in degrees and
in degrees and ![]() in meters is gib=ven by:
in meters is gib=ven by: ![]() , where
, where ![]() is the wavelength of light in meters. The largest refracting telescope in the world is at the University of chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of chicago. At a wavelength of ![]() meter, its resolution is
meter, its resolution is ![]() . Find the diameter
. Find the diameter ![]() .
.
Solution:
From the prompt:
![]()
We can re-write:![]()
We plug in the values:
![]()
Finally:![]()
Exercise 10:
Simplify ![]()
Solution:
(4) 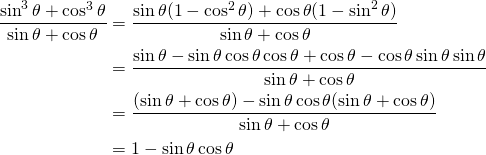
Finally:
![]()



Be the first to comment