Selected Trigonometry Exercises

Exercise 11:

A drawbridge is 150 feet long when streched across a river. The two sections of the bridge can be rotated upward through an angle of $35^{\circ}$ .

If the water level is 15 feet below the closed bridge, what is the distance $d$ between the end of a section and the water level when the bridge is fully open?

Approximaetely how far apart are the ends of the two sections when the bridge is fully opened per image?

Solution:

Distance AB is half the width of the bridge $AB=\frac{150}{2}=75$

The distance $d=y+15$

$\sin 35^{\circ}=\frac{y}{AB}$

This gives:
$y=AB\cdot \sin 35^{\circ}$
$y=75\times 0.57357644$
$y=43\; feet$

That means: $d=15+43=58\;feet$

Now For distance $x=BD$

We can see that:
$x=150-2 \times AD_{1}$

But we can see that:
$\cos 35^{\circ}=\frac{AD_{1}}{AB}$

$AD_{1}=AB\cos 35^{\circ}$
$AD_{1}=75\times 0.81915204$
$AD_{1}=61.44$

Now back to $x$

$x=150-2 \times 61.44$

$x=27.12\;feet$

Exercise 12:

Verify the following identity:

$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}}=1+\sec x \csc x$

Solution:

We have:

$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{\frac{\sin x}{\cos x}}{1-\frac{\cos x}{\sin x}}+\frac{\frac{\cos x}{\sin x}}{1-\frac{\sin x}{\cos x}}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{\sin x}{\frac{\sin x-\cos x}{\sin x}\cdot \cos x}+\frac{\cos x}{\frac{\cos x- \sin x}{\cos x}\cdot \sin x}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{\sin^{2} x}{(\sin x-\cos x)\cos x}+\frac{\cos^{2} x}{(\cos x-\sin x)\sin x}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{(1-\cos^{2} x)\sin x+(\sin^{2} x-1)\cos x}{(\sin x-\cos x)\sin x \cos x}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{\sin x- \cos^{2} x\sin x+ \sin^{2} x \cos x-\cos x}{(\sin x-\cos x)\sin x \cos x}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=\frac{\sin x-\cos x}{(\sin x-\cos x)\sin x \cos x}+\frac{(\sin x-\cos x)\sin x \cos x}{(\sin x-\cos x)\sin x \cos x}}$

$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=1+\frac{1}{\sin x \cos x}}$
$\displaystyle{\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=1+\sec x \csc x}$

Finally:
$\frac{\tan x}{1-\cot x}+\frac{\cot x}{1-\tan x}=1+\sec x \csc x$

Exercise 13:

In the following figure we can note:
$AD=x$
$AC=y$
The circle of center $O$ has a radius of $r$

Calculate the value of $y$

Calculate the distance $AB$

What relation can we get between $y$ , $x$ and $AB$ ?

If $\angle CAD=25^\circ$ :

-What is the measure of $\angle COD$ ?
-Calculate Arcs $m\stackrel\frown{CD}$ , $m\stackrel\frown{CB}$

-what relationship can we get between $\angle CAD$ , $m\stackrel\frown{CD}$ , $m\stackrel\frown{CB}$ ?

For $r=15$ :
Calculate values of $y$ and $x$

Solution:

We have the right triangle $ACO$

$y^{2}=(x+r)^{2}-r^{2}$

$y^{2}=(x+r-r)(x+r+r)$

$y^{2}=(x)(x+2r)$

For $AB$

$AB=x+r+r=x+2r$

That yields:

$y^{2}=x(x+2r)=x\cdot AB$

This confirms our relation:
$AC^{2}=AD\cdot AB$

Calculating angle $COD$ :
Angles $CAO$ and $COD$ are complementary angles:
$m\angle COD=90^{\circ}-25^{\circ}=65^{\circ}$

Central angle $COD=\stackrel\frown {CD}=65^{\circ}$

$\stackrel\frown {CD}$ and $\stackrel\frown{CB}$ are supplementary:
$\stackrel\frown{CB}=180^{\circ}-65^{\circ}=115^{\circ}$

We can see that:

$\angle CAD=\frac{1}{2}(\stackrel\frown{CB}-\stackrel\frown{CD})$

Calculating $y$

$\tan A=\frac{r}{y}$

This yields:
$y=\frac{r}{\tan A}$

$y=\frac{15}{\tan 25^{\circ}}$

$y=\frac{15}{0.46631}=32.16744$

We also have:

$\sin 25=\frac{r}{x+r}$

This gives:
$x+15=\frac{15}{\sin 25^{\circ}}$

$x=\frac{15}{0.42262}-15=20.49302$

Exercise 14:

Given:

$A=31^{\circ}$
$a=22$
$b=9$
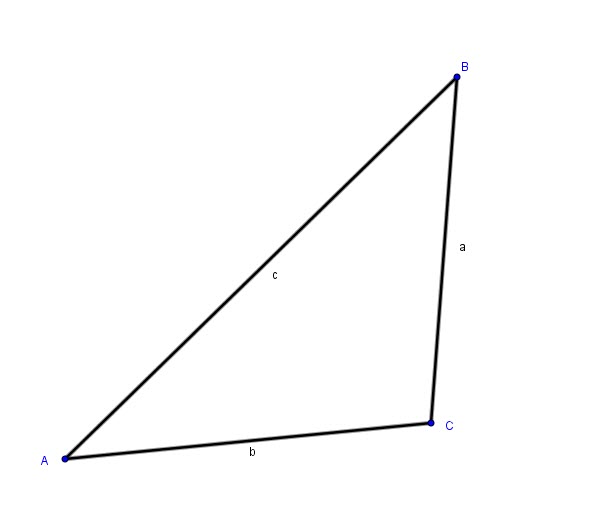
Find the other elements if the triangle is possible.

SOLUTION

ANGLES
$A=31^{\circ}$
$B=?$
$C=?$

SIDES:
$a=22$
$c=9$
$b=?$

We notice that side $a>b$ this means that $m\angle B< m\angle A$

We can safely use the LAW OF SINES:

$\frac{\sin A}{a}=\frac{\sin B}{b}\Rightarrow \sin B=\frac{b}{a}\sin A=\frac{9}{22}\sin 31=0.21070$
$m\angle B=\arcsin (0.21070)=12.16322^{\circ}$

$m\angle C=180-(31+12.16322)=136.83678^{\circ}$

For side c:
$\frac{a}{\sin A}=\frac{a}{\sin A}\Rightarrow c=\frac{a \sin C}{\sin A}=\frac{22 \sin (136.83678)}{\sin 31}=29.22063$

Answer:

ANGLES
$A=31.00000^{\circ}$
$B=12.16322^{\circ}$
$C=136.83678^{\circ}$

SIDES:
$a=22.00000$
$b=9.00000$
$c=29.22063$

We also verify that $a+b>c$ because $22+9>29.22063$

Exercise 15:

$B=160^{\circ}$
$a=19$
$b=28$
Find the other elements if the triangle is possible.

SOLUTION

[accordion hideSpeed=”300″ showSpeed=”400″]

[item title=”Click here to see the solution for Exercise 15 “]

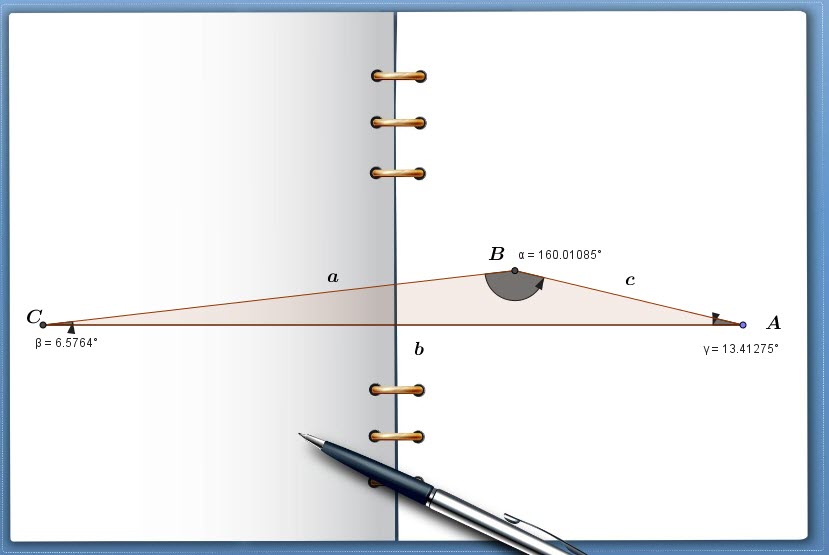
ANGLES

$A=?$

$B=160^{\circ}$

$C=?$

SIDES:
$a=19$
$b=28$
$c=?$

We notice the the sum of the measures of $\angle A$ and $\angle C$ is only $20^{\circ}$

Let’s try to calculate:

$\frac{a}{\sin A}=\frac{b}{\sin B} \Rightarrow \sin A=\frac{a}{b}\sin B=\frac{19}{28} \sin 160=0.23209 \Leftarrow m\angle A=13.42015$

$m \angle C=180-(160+13.42015)=6.57985$

$\frac{a}{\sin A}=\frac{c}{\sin C} \Rightarrow c=\frac{0.11459}{0.23209} 19=9.38089$

Answer:

ANGLES
$A=13.42015^{\circ}$
$B=160.00000^{\circ}$
$C=6.57985^{\circ}$

SIDES:
$a=19.00000$
$b=28.00000$
$c=9.38089$

Exercise 16:

$A=68^{\circ}$
$b=8$
$c=5$
Find the other elements if the triangle is possible.

SOLUTION

ANGLES
$A=68^{\circ}$
$B=?$ C=?

SIDES:
$a=?$
$b=8$
$c=5$

We notice that side $c>b$ this means that $m\angle C< m\angle B$

But in this case we don’t know if one angle is obtuse. We use the law of cosines.

Side $a$

$a^{2}=b^{2}+c^{2}-2bc \cos A$

$a^{2}=8^{2}+5^{2}-2\times 5 \times 8 \times cos 68=64+25-80 \times 0.37461=59.0312 \Rightarrow a=7.68318$

For $m\angle B:$

$b^{2}=a^{2}+c^{2}-2ac \cos B \Rightarrow \cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{7.68318^{2}+5^{2}-8^{2}}{2 \times 7.68318 \times 5}=0.26072 \Leftarrow m\angle B=74.88721$

$m\angle C=180-(68+74.88721)=37.11279$

Answer:

ANGLES
$A=68.00000^{\circ}$
$B=74.88721^{\circ}$
$C=37.11279^{\circ}$

SIDES:
$a=7.68318$
$b=8.00000$
$c=5.00000$

Exercise 17:

The following slide design is part of a water slide.

What is the total length of the shown slide having the 3 parts?

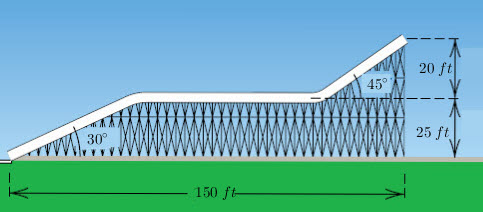
Solution:

The total distance here is the sum of the 2 hypothenuses and the horizontalpart between them.

Let $h1$ be the 1st hypothenuse, $d2$ the horizontal part and $h2$ the second hypothenuse.

For the $30^{\circ}$ angle:

$\sin 30^{\circ}=\frac{25}{h1}\Rightarrow h1=\frac{25}{\sin 30^{\circ}}$

$h1=\frac{25}{0.5}$

$h1=50\;ft$

Let the horizontal part below the angle $30^{\circ}$ be $d1$

$\tan 30^{\circ}=\frac{25}{d1}\Rightarrow d1=\frac{25}{\tan 30^{\circ}}$

$d1=\frac{25}{0.57735027}$
$d1=43.3\; ft$

For the $45^{\circ}$ angle:

$\sin 45^{\circ}=\frac{20}{h2}\Rightarrow h2=\frac{20}{\sin 45^{\circ}}$

$h2=\frac{20}{0.70710678}$

$h2=28.3\;ft$

Let the horizontal part below the angle $45^{\circ}$ be $d3$

Note that student can simply say that $d3=20\; ft$ since the triangle is isosceles.
$\tan 45^{\circ}=\frac{20}{d3}\Rightarrow d3=\frac{20}{\tan 45^{\circ}}$

$d3=\frac{20}{1}$
$d3=20\; ft$

The horizontal distance :
$d2=150-(d1+d3)=150-(43.3+20)=150-63.3=86.7\; ft$

The total Length $L$ :
$L=h1+d2+h2=50+86.7+28.3=165\; ft$

The total length of the slide is: $165\; ft$

Exercise 18:

From point $P$ , the mountaintop is viewed with an angle of elevation of $\alpha$ .From point $Q$ , located at a distance of $d$ miles due East from $P$ , the same mountaintop has an angle of elevation of $\beta$ .
verify fro figure that:
$h=\frac{d \sin \alpha \sin \beta}{\sqrt{\sin^2{\alpha}-\sin^{2}\beta}}$

What is the height of the mountain $h$ when $\alpha=30^{\circ}$ , $\beta=20^{\circ}$ and the distance $PQ=d=10\; miles$ ?

Solution:

Let $O$ be the point at the base of the mountain.

From the figure we can see that:
$\tan \alpha=\frac{h}{OP}\Rightarrow OP=\frac{h}{\tan \alpha}$

The same way:

$\tan \beta=\frac{h}{OQ}\Rightarrow OQ=\frac{h}{\tan \beta}$

But from triangle OPQ:

$d^{2}=PQ^{2}=OQ^{2}-OP^{2}$
$\displaystyle{d^{2}}=(\frac{h}{\tan \beta})^{2}-(\frac{h}{\tan \alpha})^{2}$
$\displaystyle{d^{2}}=h^{2}(\frac{1}{\tan^{2}\beta}-\frac{1}{\tan^{2}\alpha})$

This yields:

$\displaystyle{h^{2}}=\frac{d^{2}}{\frac{1}{\tan^{2}\beta}-\frac{1}{\tan^{2}\alpha}}$

$\displaystyle{h^{2}}=\frac{d^{2}}{\tan^{2}\alpha-\tan^{2}\beta}\cdot \tan^{2}\alpha\tan^{2}\beta$

$\displaystyle{h^{2}}=\frac{d^{2}}{\frac{\sin^{2}\alpha}{\cos^{2}\alpha}-\frac{\sin^{2}\beta}{\cos^{2}\beta}}\cdot \frac{\sin^{2}\alpha}{\cos^{2}\alpha}\frac{\sin^{2}\beta}{\cos^{2}\beta}$

$\displaystyle{h^{2}}=\frac{d^{2}\sin^{2}\alpha\sin^{2}\beta}{\sin^{2}\alpha\cos^{2}\beta-\sin^{2}\beta\cos^{2}\alpha}$

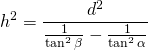
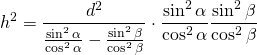
Let’s analyse the denominator:

(1) $\begin{equation*} \begin{split} \sin^{2}\alpha\cos^{2}\beta-\sin^{2}\beta\cos^{2}\alpha&=\sin^{2}\alpha(1-\sin^{2}\beta)-\sin^{2}\beta(1-\sin^{2}\alpha)\\ &=\sin^{2}\alpha-\sin^{2}\alpha\sin^{2}\beta-\sin^{2}\beta+\sin^{2}\beta\sin^{2}\alpha\\ &=\sin^{2}\alpha-\sin^{2}\beta \end{split} \end{equation*}$

Back to the equation of $h$ :
$h^{2}=\frac{d^{2}\sin^{2}\alpha\sin^{2}\beta}{\sin^{2}\alpha-\sin^{2}\beta}$

Finally:
$\displaystyle{h}=\frac{d\sin \alpha \sin \beta}{\sqrt{\sin^{2}\alpha-\sin^{2}\beta}}$

Plugging the given numbers:
$\displaystyle{h}=\frac{10\sin 30^{\circ}\sin 20^{\circ}}{\sqrt{\sin^{2} 30^{\circ}-\sin^{2} 20^{\circ}}}$

$\displaystyle{h}=\frac{10\times 0.5 \times 0.34202014}{\sqrt{(0.5)^{2}-(0.34202014)^{2}}}$

$h=4.69\;miles$

Exercise 19:

The observer of height $h$ stands on an incline at a distance $d$ from the base of a building of height $T$ , per figure. The angle of elevation from the observer to the top of the building is $\theta$ , and the incline makes an angle of $\alpha$ with the horizontal.
What is the equation of $T$ using variables $h$ , $d$ , $\alpha$ and $\theta$ ?

Using:

$h=6\;ft$

$d=50\;ft$

$\alpha=15^{\circ}$

$\theta=35^{\circ}$

find the height of the building $T$ .

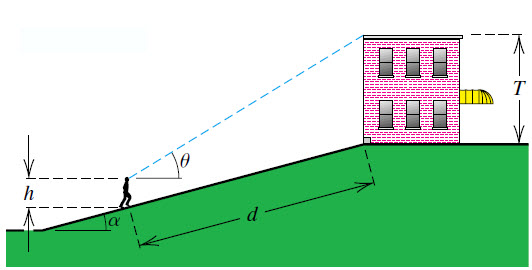
Solution:

Looking at the figure:

In triangle $GJP$ we can note that $\angle JGP=\alpha$ , corresponding angles of the transversal.

$\sin \alpha=\frac{x+h}{d}\Rightarrow x=d\sin \alpha-h$

We also have:
$\cos \alpha=frac{GP}{d}\Rightarrow GP=d\cos \alpha$

In triangle HOI:
We can see that $HI=GP=d\cos \alpha$

Also:

$\tan \theta=\frac{T+x}{HI}$

$T+x=HI\tan \theta\Rightarrow T=HI \tan \theta-x$

But $HI=d\cos \alpha$ and $x=d\sin \alpha-h$

We get:
$T=d\tan \theta \cos \alpha-d\sin \alpha+h$

Finally:

$T=h+d(\tan \theta \cos \alpha-\sin \alpha)$

Using the values:

$T=6+50(\tan 35^{\circ}\cos 15^{\circ}-\sin 15^{\circ})$

The height is:

$T=27 \; feet$

[/item] [/accordion]

Exercise 20:

A ladder of $20\:ft$ long leans against the side of a building, and the angle between the ladder and the building is $22^{\circ}$ .
Calculate the distance $d1$ from the bottom of the ladder $B$ to the building( $A$ ).

The distance from the bottom of the ladder to the building is increased by $3\; ft$ . How far does the top of the ladder move down the building?

Solution:

From the figure:
$\sin 22^{\circ}=\frac{d1}{EB}=\frac{d1}{20}$

This yields:
$d1=20\sin 22^{\circ}$

$d1=20 \times 0.37461$
$d=7.492\; ft$

From the figure we see that $d=AB$

$AC=AB+3$
$AC=7.492+3$
$AC=10.492 \; ft$

From triangle $EAB$ we have two methods to find $AE=d2+x$

We can just say that:

$\cos 22^{\circ}=\frac{d2+x}{EB}=\frac{d2+x}{20}$

This gives:

$d2+x=20\cos 22^{\circ}$
$d2+x=20\times 0.92718$
$d2+x=18.544$

Second method is the pythagorean theorem:
In triangle $EAB$ :
$d2+x=\sqrt{20^{2}-7.492^{2}}=18.544$

At this stage we can calculate angle at $D$ or simply use the pythagorean theorem. We do both:

$\sin \angle ADC=\frac{AC}{DC}$

$\sin \angle ADC=\frac{10.492}{20}$
$\sin \angle ADC=0.5246\Leftarrow \angle ADC=31.64132^{\circ}$

Now $x$ :
$\cos 31.64132^{\circ}=\frac{x}{DC}$

$x=20\cos 31.64132^{\circ}$
$x=20\times 0.85135$
$x=17.027\; ft$

The second method shows:
$x=\sqrt{20^{2}-10.492^{2}}=17.027$

But $d2+x=18.544$ from above.

This gives:
$d2=d2+x-x=18.544-17.027=1.517$

Finally:
The ladder moves down by $1.5\;ft$

Exercise 21:

Find the area of the following triangle in the figure:

Solution:

The sum of the angles is $180^{\circ}$ :

For $\angle C$ :

$m\angle C=180^{\circ}-(A+B)$

$m\angle C=180^{\circ}-(24^{\circ}10'+120^{\circ}40')$

$m\angle C=180^{\circ}-144^{\circ}50'=35^{\circ}10'$

We know that $\frac{a}{\sin A}=\frac{c}{\sin C}$

That means:

$c=a\frac{\sin C}{\sin A}$

We also know that The area can be:

$Area=\frac{1}{2}ac\sin B$

We substitute $c$ :

$Area=\frac{a^{2}\sin C \sin B}{2\sin A}$

$Area=\frac{4.25^{2}\sin 35^{\circ}10' \cdot \sin 120^{\circ}40'}{2\sin 24^{\circ}10'}$

$A=10.93\;ft^{2}$

Exercise 22:

A ladder leans against the side of a building, and the angle between the ladder and the building is $26^{\circ}$ .
After the top of the ladder was moved down the building by $2\; meters$ , the bottom of the ladder to the building was increased by $3.5\; meters$ .
What is the length of the ladder?
What angle is the new angle between the ladder and the building?
What is the distance from the bottom of the ladder to the building?

Solution:

From the figure:
$\sin 26^{\circ}=\frac{d_{1}}{y}\Rightarrow d_{1}=y\sin 26^{\circ}$

We also have:
$\cos 26^{\circ}=\frac{x+2}{y}\Rightarrow x=y\cos 26^{\circ}-2$

We can see from the figure:
$y^{2}=(d_1+3.5)^{2}+x^{2}$
$y^{2}=d_{1}^{2}+7d_{1}+12.25+(y\cos 26^{\circ}-2)^{2}$
But from above we have:
$d_{1}=y\sin 26^{\circ}$
We get:
$y^{2}=(y\sin 26^{\circ})^{2}+7(y\sin 26^{\circ})+12.25+(y\cos 26^{\circ}-2)^{2}$
$y^{2}=y^{2}\sin^{2}26^{\circ}+7y\sin 26^{\circ}+12.25+y^{2}\cos^{2}26^{\circ}-4y\cos 26^{\circ}+4$
$y^{2}=y^{2}(\sin^{2}26^{\circ}+\cos^{2}26^{\circ}+y(7\sin 26^{\circ}-4\cos 26^{\circ})+12.25+4$
$y^{2}=y^{2}+y(7\sin 26^{\circ}-4\cos 26^{\circ})+16.25$
$y(7\sin 26^{\circ}-4\cos 26^{\circ})=-16.25$
$y=\frac{16.25}{4\cos 26^{\circ}-7\sin 26^{\circ}}$

$y=\frac{16.25}{4\times 0.898794-7\times 0.438371}$

The length of the ladder is:
$y=30.859567$

Finally :
$y\approx 31\;m$

For the angle $\alpha$ :
We know that:
$d_{1}=y\sin 26^{\circ}$
$d_{1}=30.859567\times 26^{\circ}$
$d_{1}=13.52794$
The distance $AC$ is:
$d_{1}+3.5 \approx 17\;m$

The new angle $\alpha$ :
$\sin \alpha=\frac{d_{1}+3.5}{y}$
$\sin \alpha=\frac{17.52794}{30.859567}$
Used six digits to reduce the loss of accuracy.
$\sin \alpha=0.551788$
This yields:
$\alpha \approx 33.5^{\circ}$

Exercise 23:

Solve for $\theta$ when $0^{\circ}\leq \theta < 360^{\circ}$
$\sin \theta-3=5\sin \theta$

Solution:

$5\sin \theta-\sin \theta+3=0$
$4\sin \theta=-3$
$\sin \theta=-\frac{3}{4}$

The base angle hase $\frac{3}{4}$ as $sine$ value.

We get two angles here:
$\sin \gamma=\frac{3}{4}\Rightarrow \gamma=48.5904^{\circ}$

The solutions are:
$\theta_{1}=180^{\circ}+48.5904^{\circ}+k_{1}360^{\circ}=228.5904^{\circ}+k_{1}360^{\circ}$
for $k_{1}=0$ we get $\theta_{1}=228.5904^{\circ}$

$\theta_{2}=360^{\circ}-48.5904^{\circ}+k_{2}360^{\circ}=311.4096^{\circ}+k_{2}360^{\circ}$
for $k_{2}=0$ we get $\theta_{2}=311.4096^{\circ}$

when $0^{\circ}\leq \theta < 360^{\circ}$ :
Solutions:
$228.5904^{\circ}$ and $311.4096^{\circ}$
See figure.

Exercise 24:

Express $\sin 3x$ in terms of $\sin x$ only.

Solution:

(2) $\begin{equation*} \begin{split} \sin 3x&=\sin (2x+x)\\&=\sin 2x \cos x+\cos 2x \sin x\\ &=2\sin x \cos x \cos x+ (\cos^{2}x-\sin^{2}x)\sin x\\ &=2\sin x \cos^{2}x+\sin x (1-2\sin^{2}x)\\ &=2\sin x(1-\sin^{2}x+\sin x(1-2\sin^{2}x)\\ &=\sin x (2-2\sin^{2}x+1-2\sin^{2}x)\\ &=\sin x(3-4\sin^{2}x) \end{split} \end{equation*}$

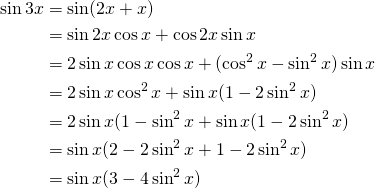
Finally:
$\sin 3x=\sin x(3-4\sin^{2}x)$

Exercise 25:

Verify:
$\cos^{4}x-\sin^{4}x=\cos 2x$

Solution:

We have:
$\cos^{4}x-\sin^{4}x=(\cos^{2}x-\sin^{2}x)(\cos^{2}x+\sin^{2}x)$

But we know that:

$\cos^{2}x+\sin^{2}x=1$

This yields:
$\cos^{4}x-\sin^{4}x=(\cos^{2}x-\sin^{2}x)$

But:
$\cos 2x=\cos^{2}x-\sin^{2} x \Rightarrow \cos^{4}x-\sin^{4}x=\cos 2x$

1 2 3 4

Post Views: 1,913

Exercise 11:

Solution:

Exercise 12:

Solution:

Exercise 13:

Solution:

Exercise 14:

SOLUTION

Exercise 15:

SOLUTION

Exercise 16:

SOLUTION

Exercise 17:

Solution:

Exercise 18:

Solution:

Exercise 19:

Solution:

Exercise 20:

Solution:

Exercise 21:

Solution:

Exercise 22:

Solution:

Exercise 23:

Solution:

Exercise 24:

Solution:

Exercise 25:

Solution:

Be the first to comment

Leave a Reply Cancel reply

Exercise 11:

Solution:

Exercise 12:

Solution:

Exercise 13:

Solution:

Exercise 14:

SOLUTION

Exercise 15:

SOLUTION

Exercise 16:

SOLUTION

Exercise 17:

Solution:

Exercise 18:

Solution:

Exercise 19:

Solution:

Exercise 20:

Solution:

Exercise 21:

Solution:

Exercise 22:

Solution:

Exercise 23:

Solution:

Exercise 24:

Solution:

Exercise 25:

Solution:

Related Articles

Solving trigonometric equations

Résolution d’Equations trigonometriques

Be the first to comment

Leave a Reply Cancel reply