Solutions de la Fonction Cubique
Beaucoup des cas qui suivent ont été déjà coverts.
Nous allons prendre le cas par cas de la fonction cubique et des solutions possibles.
Soit:
![]()
Une réduction de la fonction nous donne:
![]()
On utilise la substitution:
![]()
![]()
![]()
![]()
En simplifiant:
![]()
On met les termes semblables en facteurs et on élimine ceux qui s’ennulent.
![]()
![]()
En divisant par ![]() nous avons:
nous avons:
![]()
Et
![]()
L’Equation qui en résulte est:
![]()
A noter que quand ![]() , on peut simplement en déduire les 3 valeurs de
, on peut simplement en déduire les 3 valeurs de ![]() des valeurs de
des valeurs de ![]() .
.
Une situation idéale dans laquelle ![]() n’existe plus.
n’existe plus.
Posons:
![]()
On a:
![]()
![]()
![]()
Nous voyons que:
![]() and
and ![]() pourra ennuler l’équation.
pourra ennuler l’équation.
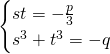
En élévant au cube:
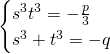
Soit maintenant:
![]() and
and ![]()
Nous avons:
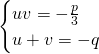
Pour la résolution nous aurons:
![]()
If ![]() , the equation has one real root and 2 complex roots
, the equation has one real root and 2 complex roots
If ![]() , the equation has one root
, the equation has one root ![]() and a double root
and a double root ![]()
If ![]() , the equation has three real roots
, the equation has three real roots
Le Cas: 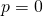
![]()
Racines complexes:
![]()
![]()
![]() with
with ![]()
If ![]()
Nous obtenons:
![]()
![]()
![]()
![]()
Le Cas: 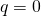
![]()
![]()
![]()
if ![]()
![]()
![]()
![]()
![]()
![]()
Si ![]()
![]()
![]()
![]()
![]()
![]()
Le Cas: 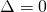
![]()
Qui signifie que:
![]() Meaning
Meaning ![]()
Nous obtenons les solutions suivantes:
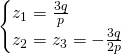
Nous utilisons:
![]() to get
to get ![]()
Le Cas 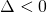
Nous procedons comme suit:
![]()
Quand on remplace ![]() dans l’équation:
dans l’équation:
![]()
![]()
![]()
![]()
Une simple division donne:
![]()
Nous simplifions le membre de gauche:
(1) 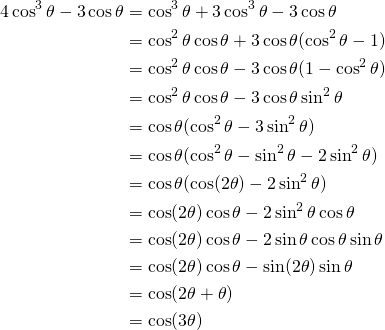
On en déduit que:
![]()
Si nous posons:
![]()
De notre Equation nous aurons:
![]()
En remplaçant:
![]()
![]()
Les mêmes techniques nous donnent:
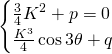
![]()
![]()
![]()
![]() Remember
Remember ![]()
![]() with
with ![]()
Les Solutions:
![]()
![]()
![]()
Nous pouvons en déduire les valeurs de ![]() .
.
![]()
![]()
![]()
Le Cas: 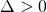
Avec 
Nous obtenons:
![]()
La même transformation nous donne:
![]()
Et par la suite:
![]()
Avec 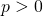
Nous obtenons
![]()
La même transformation nous donne:
![]()
Et puis:
![]()
Règle Générale por toutes les solutions y compris les complexes conjugués:
De l’Equation:
![]()
Avec:
![]()
Premier cas: Avec 
On calcule ![]() and
and ![]()
![]()
Maintenant:
![]()
Les valeurs de ![]() :
:
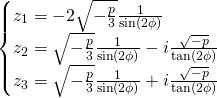
Pour les valeurs de ![]() nous effectuons
nous effectuons ![]()
Second cas: Avec 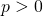
Nous calculons ![]() and
and ![]()
![]()
Maintenant:
![]()
Les valeurs de ![]() :
:
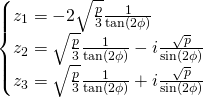
Pour les valeurs de ![]() nous effectuons
nous effectuons ![]()
Exemple 1:
Trouver les solutions de:
![]()
Solution:
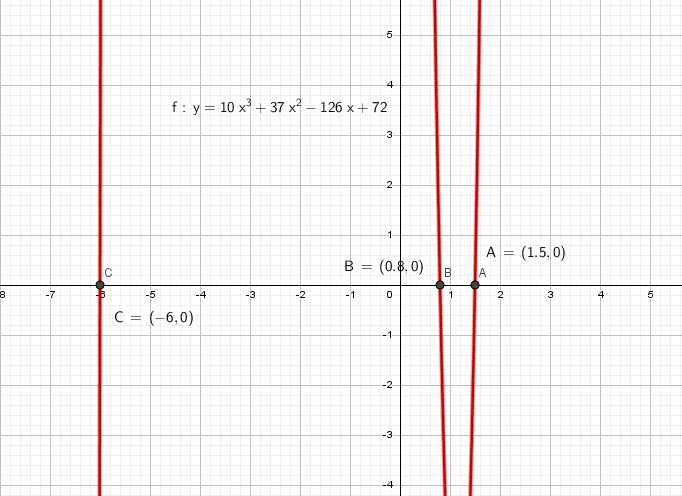
Au lieu de faire des essais multiples entre 72 et 10 avec leurs facteurs premiers, nous allons appliquer les méthodes ci-dessus.
Pour éviter les grands nombres, divisons l’équation par 10.
Nous avons:
![]()
Nous avons les coefficients suivants:
![]()
![]()
![]()
![]()
Calculons ![]() et
et ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Gardons la forme fractionnaire pour ne pas perdre la précision.
Maintenant:
![]()
![]()
![]()
C’est le cas: ![]()
Utilisons la méthode équivalente:
![]()
![]()
![]() in degrees
in degrees
![]()
![]()
![]()
Les solutions:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalement les solutions sont:
Réponse: ![]() ,
, ![]() and
and ![]()
Exemple 2:
Trouver les solutions de:
![]()
Solution:
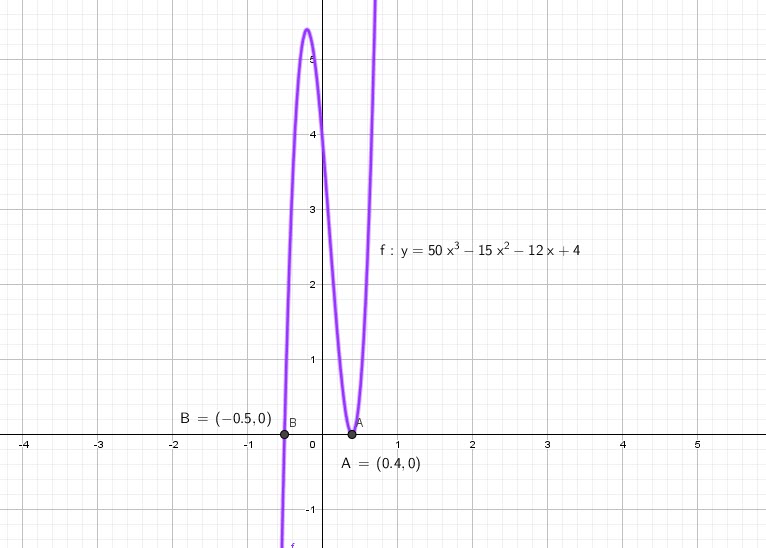
Au lieu de faire des essais multiples entre 4 et 50 avec leurs facteurs premiers, nous allons appliquer les méthodes ci-dessus.
Pour éviter les grands nombres, divisons l’équation par 50.
Nous avons:
![]()
Nous avons les coefficients suivants:
![]()
![]()
![]()
![]()
Calculons ![]() and
and ![]()
![]()
![]()
On remplace
![]()
![]()
![]()
L’exposent ![]() n’existe plus.
n’existe plus.
![]()
![]()
Ici:
![]()
![]()
Examinons la valeur de ![]()
![]()
![]()
![]()
C’est le cas où ![]()
Nous avons les solutions suivantes:
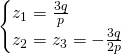
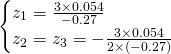
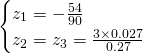
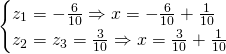
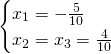
Finalement les solutions sont:
Réponse: ![]() ,
, ![]() and
and ![]()
Exemple 3:
Trouver les solutions de:
![]()
Solution:
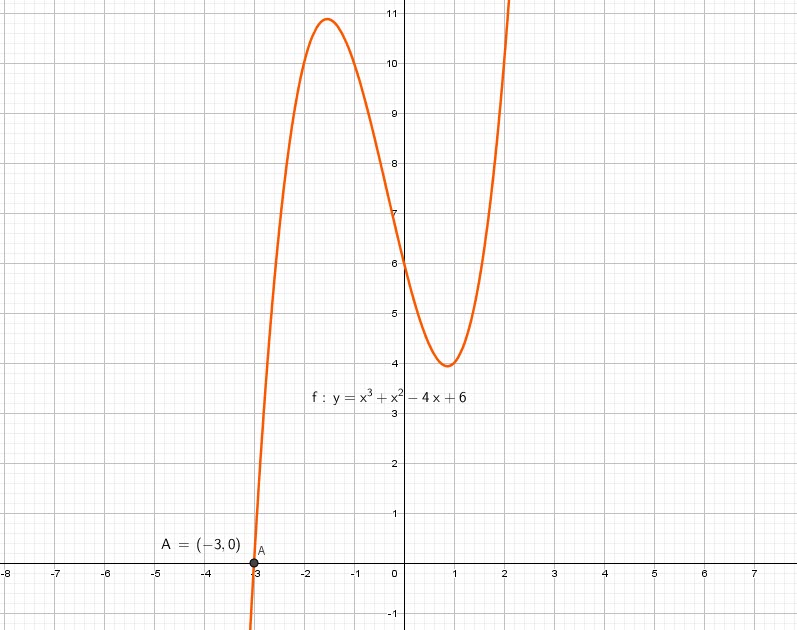
Au lieu de faire des essais multiples entre 6 et 1 avec leurs facteurs premiers, nous allons appliquer les méthodes ci-dessus.
Nous avons les coefficients suivants:
![]()
![]()
![]()
![]()
Calculons ![]() and
and ![]()
![]()
![]()
On remplace:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si ![]() , l’équation a une racine réelle et deux racines complexes.
, l’équation a une racine réelle et deux racines complexes.
![]()
Calculons ![]() and
and ![]()
![]()
![]()
![]()
Maintenant:
![]()
![]()
![]()
Les valeurs de ![]() :
:
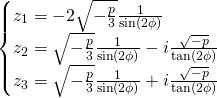
Pour les valeurs de ![]() :
:
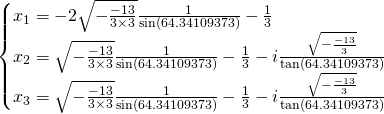
Nous avons
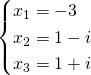
Finalement les solutions sont:
Réponse: ![]() ,
, ![]() and
and ![]()
Autres méthodes par division
Voir les documents qui suivent:
Exemple 1:
Trouver les solutions de:
![]()
Solution:
Exemple 2:
Trouver les solutions de:
![]()
Solution:
Exemple 3:
Trouver les solutions de:
![]()
Solution:

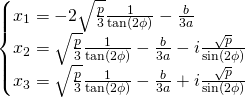

Be the first to comment