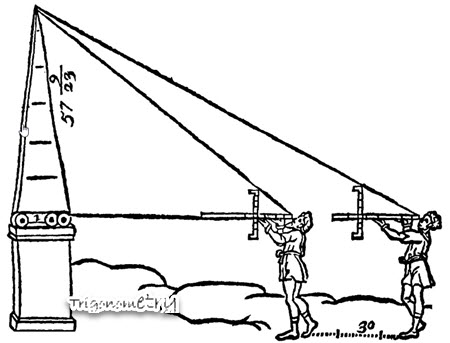

Résolution d’Equations trigonometriques
Angle d’élevation:
On rencontre le mot “Angle d’Elevation” dans beaucoup de problèmes de trigonométrie.
L’angle d’élevation d’un objet est l’angle formé entre l’horizontale et la demie-droite passant par cet objet. Le sommet de l’angle étant le point d’observation ou oeil de l’observateur.
L’observateur lève la tête pour regarder l’objet
Sur cette figurel’ ![]() ou
ou ![]() constitue l’angle d’élevation.
constitue l’angle d’élevation.

Angle de depression:
L’angle de depression d’un objet est formé par l’horizontale passant par l’observateur et la demie-droite passant par l’objet.
Ici l’observateur doit regarder en bas pour voir l’objet.
Sur la figure l’ ![]() ou
ou ![]() est l’angle de depression.
est l’angle de depression.

Formules du triangle rectangle
Nous avions vu ces formules avec le cercle trigonométrique.
La seule difference est que l’hypoténuse n’est pratiquement jamais égale à ![]() .
.
On peut cependant diviser tous les côtés par l’hypoténuse on aura:
Pour un angle non-droit du triangle:
![]() pour le cercle trigonométrique.
pour le cercle trigonométrique.
![]() pour le cercle trigonométrique.
pour le cercle trigonométrique.
Ces deux formules deviennent:
La tangente ne change pas:
Beaucoup d’exercices en trigonométrie trouvent leur solution avec ces formules.
Ceci nous montre qu’en divisant un triangle quelconque en 2 triangles rectangles, on pourra trouver la solution en utilisant ces formules.
Fonctions trigonométriques inverses:
Toutes les fonctions trigonométriques ont leur inverse.
Ces fonctions sont de la forme:
Si ![]() , On peut écrire cette coreespondance
, On peut écrire cette coreespondance ![]() .
.
On y reviendra.
Pour ![]() nous avons:
nous avons:
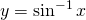 for
for 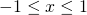 and
and 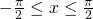
Nous avons la propriété:
![]() si
si ![]()
![]() si
si ![]()
Exemple:
Trouver ![]() pour:
pour:
![]()
![]()
![]()
Pour ![]() nous avons:
nous avons:
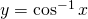 for
for 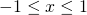 and
and 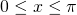
A lire “y est l’inverse cosinus de x” ou arccosinus
Nous avons la propriété:
![]() si
si ![]()
![]() si
si ![]()
Pour ![]() nous avons:
nous avons:
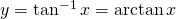 iff
iff 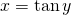
Pour tout 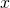 et pour
et pour 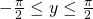
A lire “y est l’inverse tangente de x” ou arctangente
Nous avons la propriété:
![]() pour tout
pour tout ![]()
![]() si
si ![]()
Exemple:
Trouver la valeur de:
Si ![]() nous pouvons avoir
nous pouvons avoir ![]()
Ici l’hypoténuse est de ![]() .
.
Maintenant :
![]()
![]()
Si ![]() nous pouvons avoir
nous pouvons avoir ![]()
L’hypoténuse est de ![]() .
.
Maintenant:
![]()
Nous avons besoin de ![]()
![]()
Après simplification nous aurons:
![]()



Be the first to comment