Spherical trigonometry
The spherical trigonometry is the branch of spherical geometry which deals with spherical triangles defined by great circles on the sphere.
It allows us to calculate the trigonometric functions of the sides and angles of these spherical polygons.
A great circle on the sphere is any circle having its center as the center of the sphere.
The spherical polygon is a polygon on the surface of the sphere defined by great-circle arcs.
The angles of proper spherical triangle are less than ![]()
This means ![]()
The same for the sides:
The sides of proper spherical triangle are less than ![]()
This means ![]()
Spherical law of cosines
Cosine rule for sides:
![]()
When ![]()
We get:
![]()
The formula becomes
![]()
Cosine rule for angles:
![]()
Both of these formulae can be rearranged to get ![]() or
or ![]()
Spherical Law of Sine:
![]()
Half-side Formula:
In a spherical triangle:
![]()
![]()
![]()
![]() is half the sum of the angles:
is half the sum of the angles:
![]()
Also:
![]()
Cotangents formula:(4 consecutive elements)
If we write:
![]()
Dividing by ![]() and using sine rule we get:
and using sine rule we get:
![]()
Formula involving half-angles and half-sides:
If we let:
![]() the semi-perimeter of the triangle.
the semi-perimeter of the triangle.
![]()
If ![]()
![]()
Gauss Formulas:
![]()
AND
![]()
OR:
![]()
AND
![]()
Leading to:
![]()
Napier Formulas:
Obtained from Gauss’s Formulas:
![]()
![]()
![]()
![]()
Spherical triangle area:
This is called the GIRARD formula. Using the difference of the sum of the angles of the triangle and ![]()
If ![]() is the Radius of the sphere, the Area in STERADIANS (From angles in RADIANS) is:
is the Radius of the sphere, the Area in STERADIANS (From angles in RADIANS) is:
![]()
Solving Spherical Triangles:
It should be known that the SPHERICAL EXCESS ![]() where
where ![]() is the Area of the triangle and
is the Area of the triangle and ![]() is the radius of the Sphere.
is the radius of the Sphere.
Given the 3 sides  ,
, 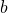 and
and  :
:
For angle ![]()
![]()
For angle ![]()
![]()
For angle ![]()
![]()
![]()
With:
![]()
Given one angle with 2 adjacent sides:
Example, Given ![]() ,
, ![]() and
and ![]()
The side ![]() :
:
![]()
For Angle ![]() we use Napier’s Analogies:
we use Napier’s Analogies:
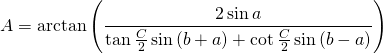
For Angle ![]() we use Napier’s Analogies:
we use Napier’s Analogies:
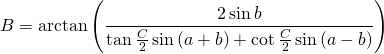
Same goes for the Excess ![]() :
:
Given one angle its opposite side and one adjacent side:
Example, Given ![]() ,
, ![]() and
and ![]()
Using the Napier’s formulas there is solution only if;
![]()
We get:
For angle ![]() :
:
![]()
For side ![]() :
:
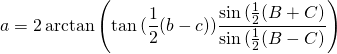
For angle ![]() :
:
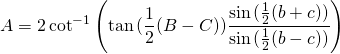
For the Excess ![]() :
:
![]()
Another solution when ![]() and
and ![]() is an acute angle:
is an acute angle:
![]()
Two angles and an included side:
If we know ![]() and
and ![]() with included side
with included side ![]() .
.
![]()
![]()
![]()
![]()
Two angles and a non-included side:
If we know angles ![]() ,
, ![]() and an opposite side of one of the two angles, let’s say side
and an opposite side of one of the two angles, let’s say side ![]() :
:
![]()
![]()
![]()
![]()
if ![]() is acute and
is acute and ![]() there is another solution.
there is another solution.
![]()
Three angles:
![]()
![]()
![]()
![]()


Be the first to comment