Sum and difference formulas

We have seen in the past cases where we had to use these sum and difference formulas. At this stage, we are now exploring them to be able to use them even better.

Now that we know how to identify functions of a given angle. Now we’ll see what those functions are when two angles are added and when two angles are subtracted.

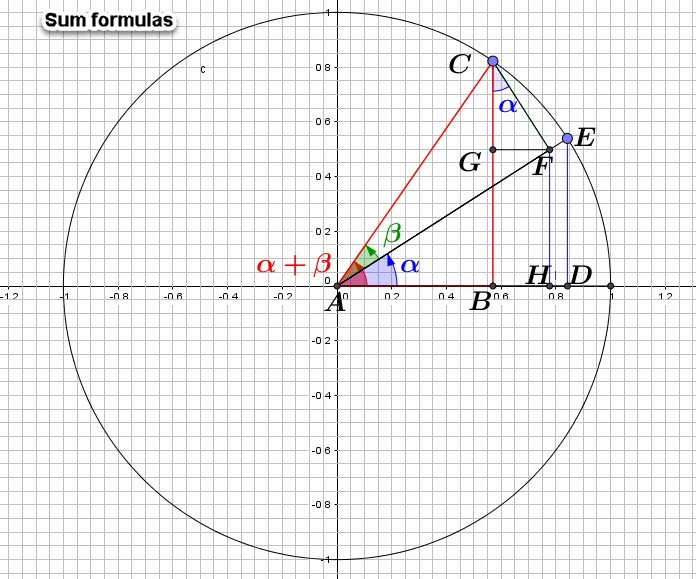
Let’s take two angles $\alpha$ and $\beta$ and use some of well-known “postulates” fro Geometry.

Angle $\alpha$ is in $\triangle DAE$

Angle $\beta$ is in $\triangle FAC$

Angle $\alpha+ \beta$ is in $\triangle BAC$

We know that:
$\sin (\alpha+ \beta)=BC$

But we can see that $BC=BG+GC$

$\cos \alpha=\frac{AH}{AF}$

$\sin \beta=FC$

But from $\triangle GCF$ we have:
$\cos \alpha=\frac{GC}{FC}=\frac{GC}{\sin \beta}\Rightarrow GC=\sin \beta \cdot \cos \alpha$

From $\triangle HAF$ we can see that:
$\sin \alpha=\frac{HF}{AF}$

From $\triangle FAC$ we can see that:
$\cos \beta=AF$

That yields:
$\sin \alpha=\frac{HF}{\cos \beta} \Rightarrow HF=\sin \alpha \cdot \cos \beta$

We can also see that: $BG=HF$

Finally:
$\sin (\alpha+ \beta)=BC=BG+GC=\sin \alpha \cdot \cos \beta+\sin \beta \cdot \cos \alpha$

$\sin (\alpha+\beta)=\sin {\alpha}\cos \beta+ \cos {\alpha} \sin \beta$

Sum and difference formulas using distances

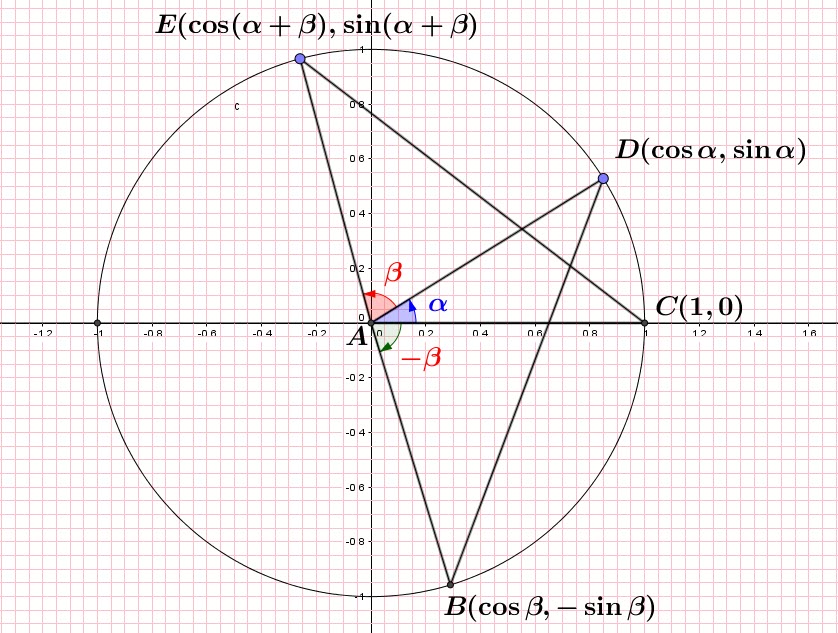
We should remember that the distance between two points is:

$d=\sqrt{(X_2-X1)^{2}+(Y_2-Y1)^{2}}$ where the coordinates pairs are $(X_1,Y_1)$ and $X_2,Y_2)$

In the following figure:

$\triangle BAD \cong \triangle CAE$

$(BD)^{2}=(CE)^{2}$ by CPCTC

$(\cos \alpha-\cos \beta)^{2}+(\sin \alpha+\sin \beta)^{2}=(\cos (\alpha+\beta)-1)^{2}+(\sin (\alpha+\beta))^{2}$

$\cos^{2} \alpha-2\cos \alpha \cos \beta+\cos^{2}\beta+ \sin^{2}\alpha+2\sin \alpha \sin \beta+\sin^{2}\beta=\cos^{2} (\alpha +\beta)-2\cos (\alpha+\beta)+1+\sin^{2} (\alpha +\beta)$

Simplifying:
$2-2\cos \alpha \cos \beta+ 2\sin \alpha \sin \beta=-2\cos (\alpha+\beta)+2$

This yields:

$\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$

Using complex numbers and the de Moivre’s formula

Before we proceed, it should be noted that for two complex numbers to be equal, the real parts must be equal and the imaginary parts must be equal.

$z=a+bi$

$z'=a'+b'i$

$a=a'\; and \; b=b' \Rightarrow z=z'$

We know that $z=e^{i\alpha}=\cos \alpha+ i\sin \alpha$

$z'=e^{i\beta}=\cos \beta+ i\sin \beta$

$zz'=e^{i\alpha}e^{i\beta}=e^{i(\alpha+\beta)}=\cos (\alpha+\beta)+ i\sin (\alpha+\beta)$

Also:

$zz'=(\cos \alpha+ i\sin \alpha)(\cos \beta+ i\sin \beta)=\cos \alpha \cos \beta+i^{2}\sin \alpha \sin \beta+i(\sin \alpha \cos \beta+\cos \alpha \sin \beta)$