The passing Airplane

A navigator on board a ship at anchormeasures the angle of inclination of 28 degrees to an approaching airplane at exactly 10:59:50Hrs. The altitude of the plane at that time is 5800 feet. At 11:00:15 Hrs, the navigator takes another

measurement of 53 degrees as angle of inclination. According to the communications, the plane has started the descent to land at a nearby airport. The descent is 32.8 feet every second and it will remain constant. The plane will have the same spped during the observation.

1. What is the speed of the airplane in km/h? Round to the tenth.
2. At what time and altitude, in meters, the plane will be above the navigator. Please round the distance to the meter and the time to the tenth of a second?
3. The visibility is 15,000 feet. At what time the plane will be out of sight? Round to the tenth of a Second.
4. What is the angle of elevation at the time found in question 3?
5. What is the altitude of the plane, in meters, when it is about to be disappear from the observator binoculars?
6. What is the total distance, in meters, traveled by the plane for the duration of the observation? Round the answer to the meter.
The ground is even. Please use1 meter=3.28 feet.
1km=1000 m.

Guided solution:

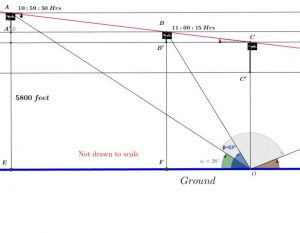
While putting this problem together, we tried to make the student use the maximum number of tools learned so far.

Question 1: What is the speed of the airplane in km/h? Round to the tenth

Looking at the figure in this solution, we know that we can find the time between A and B.
Using time calculation, we can find the answer:

Two ways:

At A we need 10 seconds to reach 11:00:00 Hrs. The plane reaches B 15 seconds after 11:00:00Hrs.
Total 10seconds+15 seconds=25 seconds.
Aternate Way
$T_B=11 \times 3600+0 \times 60+15=39615\;seconds$
$T_A=10 \times 3600+59\times 60+50=39590\;seconds$
Now the time difference:
$t=39615-39590=25 \; seconds$

The descent is $32.8\frac{feet}{second}$
We convert: $\frac{1\;m}{3.28\;ft}=\frac{x\; m}{32.8\;ft}$
With our knowledge on proportions: $32.8\;ft=10\;m$
We also get altitude $EA=5,800\;ft=1768\;m$

Finding distance AB:

We have the total descent:
$AA'&=25\times 10 =250\;m$
From our $\triangle AA'B$ we have $AB=\sqrt{{AA'}^2+{A'B}^2}$
But $\overline{A'B}=\overline{EF}$
We also see that from the segment addition postulate:
$\overline{EO}=\overline{EF}+\overline{FO}$
We get
$EO=EF+FO\Rightarrow EF=EO-FO$
$\tan{\alpha}=\frac{AE}{EO} \Rightarrow EO=\frac{AE}{\tan{\alpha}}$
$EO=\frac{1768}{\tan{28^\circ}}=3325\;m$
We now calculate $FO$ but:
$\tan{\beta}=\frac{BF}{FO} \Rightarrow FO=\frac{BF}{\tan{\beta}}$

But we know:
$BF=A'E=AE-AA'=1768-250=1518\;m$
For $FO$ :
$FO=\frac{BF}{\tan{\beta}}=\frac{1518}{\tan{53 ^\circ}}=\frac{1518}{1.327}=1144\;m$

For $EF$ :

$EF=A'B=EO-FO=3325-1144=2181\;m$
Also:
$\tan{\angle{A'BA}}=\frac{AA'}{A'B}=\frac{250}{2181}=0114626$
$\angle{A'BA}=6.5391^\circ$

Now to calculate AB, we have two ways:

$\sin{\angle{A'BA}}=\frac{AA'}{AB} \Rightarrow AB=\frac{AA'}{\sin{\angle{A'BA}}}$
$AB=\frac{250}{\sin{6.5391^ \circ}}=2195\;m$

$AB=\sqrt{{AA'}^2+{A'B}^2}=\sqrt{{250}^2+{2181}^2 }=2195\; m$

Now the speed: one hour is 3600 seconds
$25 \;seconds \longrightarrow 2.195 \;km$
$3600 \;seconds \longrightarrow x \;km$
$x=\frac{3600 \times 2.195}{25}=316.1\;km/h$

Answer: the plane is flying at a speed of $316.1\;km/h$

Question 2: At what time and altitude, in meters, the plane will be above the navigator. Please round the distance to the meter and the time to the tenth of a second?

On the graph, from $\triangle{BFO}$ we have:

$sin{\beta}=\frac{BF}{OB}\Rightarrow OB=\frac{BF}{\sin{\beta}}$
$OB=\frac{1518}{\sin{53^\circ}}=1901\;m$

Alternate way to OB
${OB}^2={FO}^2+{BF}^2$

$OB=\sqrt{{1144}^2+{1518}^2}\\&=1901\; m$

$m \angle{BOC}=90 ^\circ-53^ \circ=37 ^\circ$
$m \angle{BCO}=90^\circ+ m\angle{BCB'}$
But this plane is following a transversal to all these parallel lines.
$m \angle{BCB'}=m \angle{A'BA}$
$m \angle{BCO}=90^ \circ+6.5391^ \circ=96.5391^ \circ$

From the graph:
$\frac{\sin{\angle{BOC}}}{BC}= \frac{\sin{\angle{BCO}}}{OB}$

$BC=OB \cdot \frac{\sin{\angle{BOC}}}{\sin{\angle{BCO}}}= 1901 \cdot \frac{\sin{37^ \circ}}{\sin{96.5391 ^\circ}}=1152 \;m$
The distance traveled is $1.152 \;km$

The time:
$t=\frac{1.152\;km \times 3600\;seconds}{316.1 \;km}=13.1\; seconds$

Finally: The plane will be overhead at11:00:28.1 Hrs

We just added the 13.1 seconds to the 15 seconds after 11:00 Hrs.

Shorter path for question 2
$\tan{\angle{B'CB}}=\frac{BB'}{B'C}$
But we know that:
$B'C=OF \Rightarrow \tan{}\angle{B'CB}=\frac{BB'}{OF}$
$BB'=1144 \times \tan{6.5391^\circ}=131\;m$
Descent is 10 m per second. Time of descent is $t=\frac{131}{10}$
We end up with the same answer of 13.1 seconds.

Altitude when overhead:
Distance OC

$OC=FB-BB'=1518-131=1387\;m$

Answer: the altitude will be $1387\;m$ when overhead.

Question 3: The visibility is 15,000 feet. At what time the plane will be out of sight? Round to the tenth of a second.

$m\angle{OCD}=90^\circ-6.5391^ \circ=83.4609 ^\circ$
$OD=15,000\;feet\\&=4573 \;m$

$\frac{\sin{\angle{OCD}}}{OD}= \frac{\sin{\angle{ODC}}}{OC}$
$\sin{\angle{ODC}}= OC\cdot \frac{\sin{\angle{OCD}}}{OD}= 1387 \cdot \frac{\sin{83.4609^ \circ}}{4573}=0.30133$
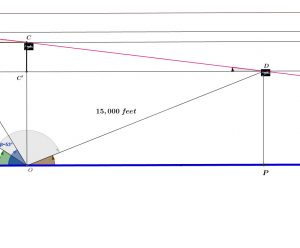
We find: $m\angle{ODC}=17.5374^ \circ$
We also have:
$m\angle{COD}=180^\circ-83.4609^\circ+17.5374^\circ)=79.0017^\circ$
Now we can progress towards finding CD:
$\frac{\sin{\angle{COD}}}{CD}= \frac{\sin{\angle{OCD}}}{OD}$
$CD=OD \times \frac{\sin{\angle{OCD}} }{\sin{\angle{OCD}}}= 4573 \times \frac{\sin{79.0017 ^\circ} }{\sin{83.4609 ^\circ}}=4518 \;m=4.518\;km$
The time it takes to travel CD:
$t=\frac{4.518 \times 3600}{316.1}=51.5\;seconds$
Adding this time to $T_B=11:00:28.1\;Hrs$ we get:

Answer: Time when plane ceases to be observed: $T_D=11:01:19.6 Hrs$

Question 4: What is the angle of elevation at the time found in question 3?

We have to find $m\angle{DOP}$
$m\angle{DOP}=90 ^\circ-m\angle{COD}=90^\circ-79.0017 ^\circ=10.9983 ^\circ\approx 11 ^\circ$

Answer: Angle of elevation is $11^ \circ$

Question 5: What is the altitude of the plane, in meters, when it is about to be disappear from the observator binoculars?

We need to calculate $DP$ .
Too many ways
$\sin{\angle{DOP}}=\frac{DP}{OD} \Rightarrow DP=OD \cdot \sin{\angle{DOP}}$
$DP=4573 \cdot \sin{10.9983^ \circ}=872\;m$

Answer: The altitude of the plane is: $872 \;m$

Question 6: What is the total distance, in meters, traveled by the plane for the duration of the observation? Round the answer to the meter.

Too many ways here :

Method 1:

Total Descent:
At $A$ the altitude is $1768 \;m$
Total descent: $1768-872=896$
Time to descend: $\frac{896}{10}=89.6 \; seconds$
That matches our time difference between D and A positions.
Now the distance is:
$Dist=\frac{89.6 \times 316.1}{3600}=7.867\;km=7,867\;m$

Answer: the total distance is: $7,867\;m$

Method 2:

$Dist=AB+BC+CD=2,195+1,152+4,518=7865\;m$
Slightly different due to successive roundings.

Method 3:

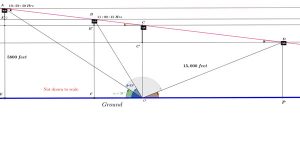
With $\triangle AOD$ :
$m \angle{OAD}=21.4609$
$m \angle{AOD}=141.0017$
$m \angle{ADO}=17.5374$
$OA=\sqrt{{EA}^2+{OE}^2}=\sqrt{{1768}^2+{3325}^2}=3766 \;m$
Now we use:
$AD=\sqrt{{OA}^2+{OD}^2-2 \cdot (OA)\cdot (OD) \cdot cos{\angle {AOD}}}= \sqrt{{3766}^2+{4573}^2-2 \cdot (3766)\cdot (4573) \cdot cos{141.0017^\circ}}=7865\;m$