Trigonometric functions: Tangent of an angle

We are following our introduction to the trigonometric functions.
It was necessary to go through some reminders in geometry to be able to understand the next topics in Trigonometry.
We covered topics like proportions in Algebra et similarities and circles in Geometry. We will need some of that knowledge in explaining the next trigonometric functions.
We know how to identify the $sine$ and $cosine$ of an angle. We are now going to introduce the tangent.

In the following figure, we take $\overline{BE}$ as the $tangent$ of the central angle with $B$ as the point of tangency.
$\tan(\alpha)=BE$
We can see how this function changes with the central angle.

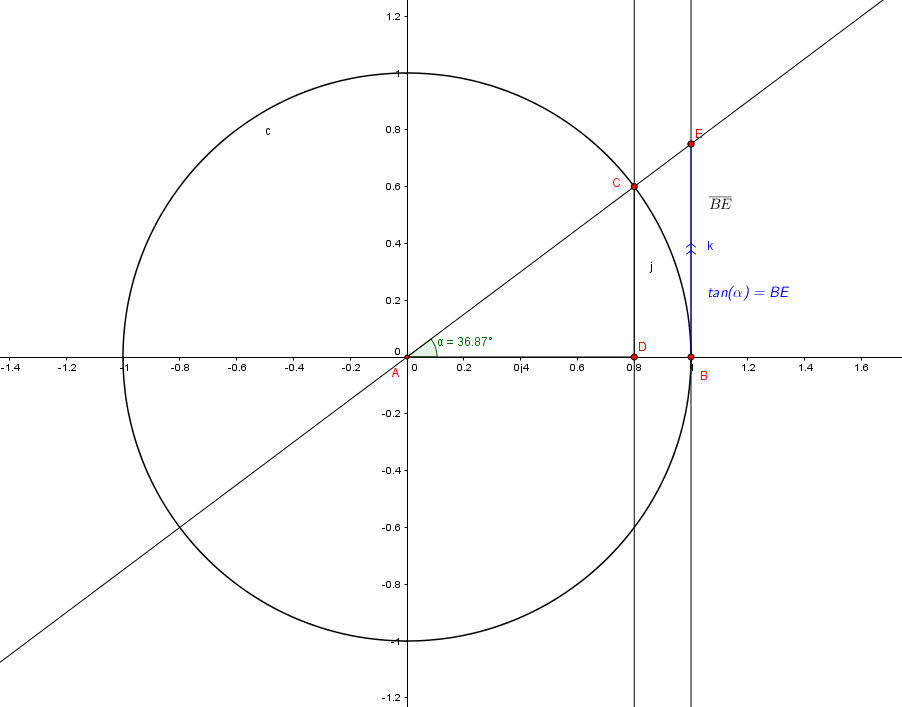
We can see that triangles ADC and ABE are similar
$\triangle ADC \sim \triangle ABE$
From similarities:
$\frac{BE}{DC}=\frac{AB}{AD}$
But we know that:
$DC$ is the $\sin(\alpha)$
$AD$ is the $\cos(\alpha)$
$AB=1$ , radius of our circle.
We can now write:
$\frac{\tan(\alpha)}{\sin(\alpha)}=\frac{1}{\cos(\alpha)}$
And we get the know relationship:

$\tan(\alpha)=\frac{sin(\alpha)}{\cos(\alpha)}$

Before we close this lesson, we can get ahead of ourselves and introduce blindly another trigonometric function.

We can see from the graph, using similarity properties, that:
$\frac{AE}{AC}=\frac{AB}{AD}$
But we can also see in triangle ABE that:
$(AE)^{2}=(BE)^{2}+1$
Our relation becomes:
$AE=\frac{1}{\cos(\alpha)}$
And