Elementary trigonometric functions

After having introduced the first three trigonometric functions of a given angle , now we are going to introduce their reciprocals.

Secant:

This is the reciprocal of the noted .

Let’s look at the following graph.

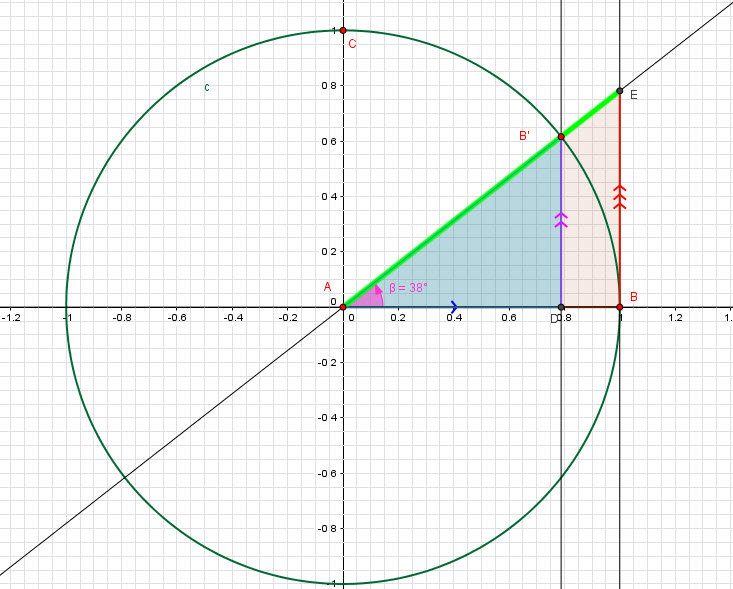
Finally the is:

Cosecant:

This is the reciprocal of the noted .

Let’s look at the following graph.

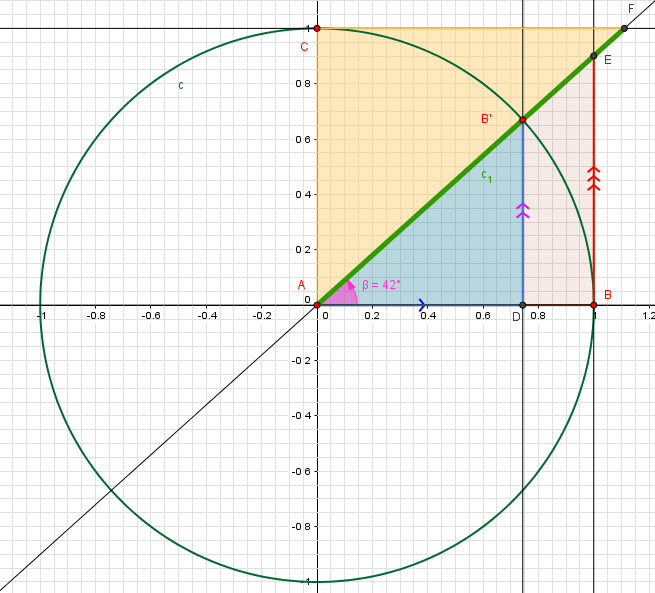
by AA

Finally the is:

Cotangent:

This is the reciprocal of the noted .

Let’s look at the following graph.

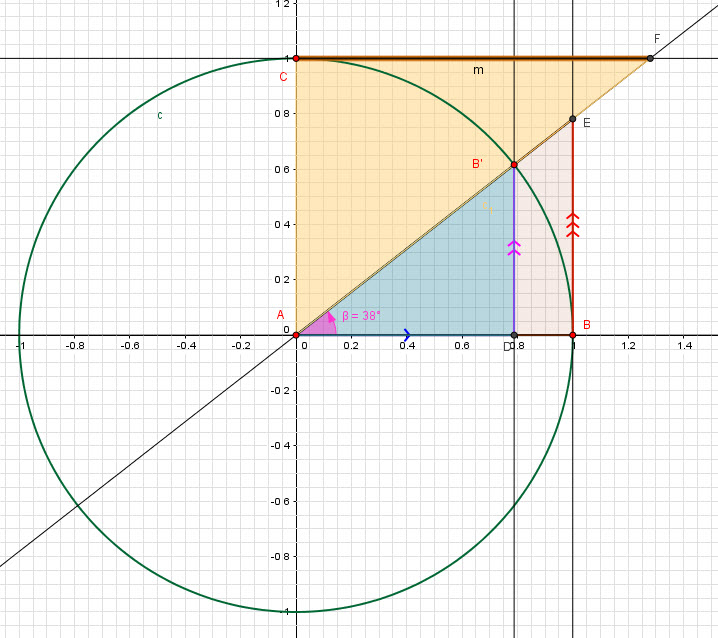
by AA

Finally the is:

We can also see that:

by AA

We get:

Finally: