Truncated Cone Area and Volume
Truncated Cone Area and Volume
A truncated cone is the result of cutting an entire cone by a plane parallel to the base and removing the part containing the apex.
The height ![]() is the distance
is the distance ![]() between the centers of the bases.
between the centers of the bases.
Area of the truncated cone or frustum
To calculate the area of the truncated cone, we will consider the two cones:
-The entire cone with Base ![]() and apex
and apex ![]()
-The removed cone with Base ![]() and apex
and apex ![]()
-The difference will help calculate the lateral area and later the volume of the truncated cone.
The 2 slants:
![]()
![]()
TheLateral Areas:
![]()
For the removed cone:
![]()
The Lateral Area:
(1) 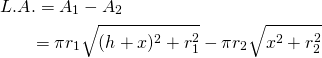
-Let’s find ![]()
From the similar triangles above:
![]()
This yields:
![]()
![]()
![]()
![]()
Back to the Lateral Area:
(2) 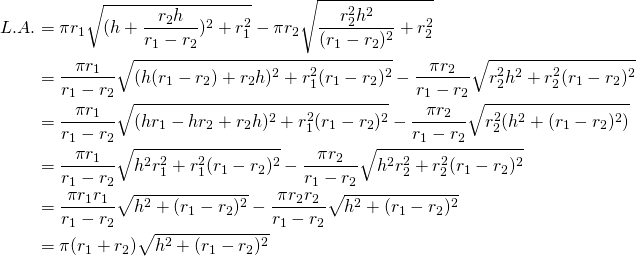
Finally:
![]()
Area of the Base:
![]()
![]()
The Total Area:
Volume of the truncated cone:(Frustum)
We already found the expression of ![]()
The volume follows the same method of substracting the two cones:
The volume of the cone is:
![]()
We have two cones here:
The cone with base ![]()
![]()
And the cone with Base ![]()
![]()
The volume of the frustum:
![]()
![]()
![]()
![]()
With the expression of ![]()
![]()
![]()
![]()
![]()
Back to the volume of the frustum
![]()
![]()
![]()
Finally:


Be the first to comment