Unit Circle, important angles

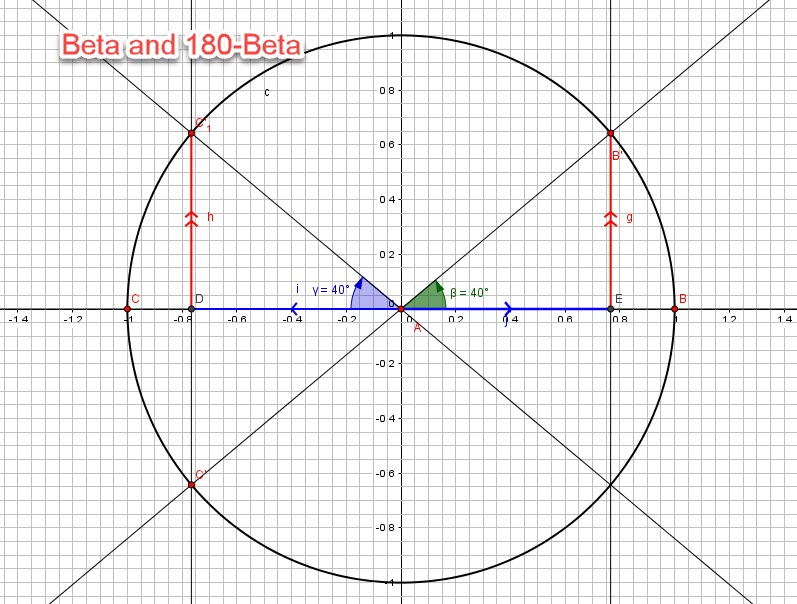
Supplementary angles

It has been said that supplementary angles have their sum $\pi\; or\; 180^\circ$

Looking at the following figure, we can see that $\triangle AEB' \cong \triangle ADC_1$ by the AAS postulate.

$\angle EAB' =\angle DAC_1$

The actual angle is $\pi-\beta$

$\sin (\pi-\beta)=DC_1$

However, by CPCTC, $DC_1=EB'=\sin \beta$

We also notice that $\cos (\pi-\beta)=AD=-AE=-cos \beta$ by CPCTC

This shows that:

To avoid repetition we know that $\pi-\alpha=\frac{\pi}{2}+(\frac{\pi}{2}-\alpha)$

This opens up the following:

1 2 3 4 5

Post Views: 648